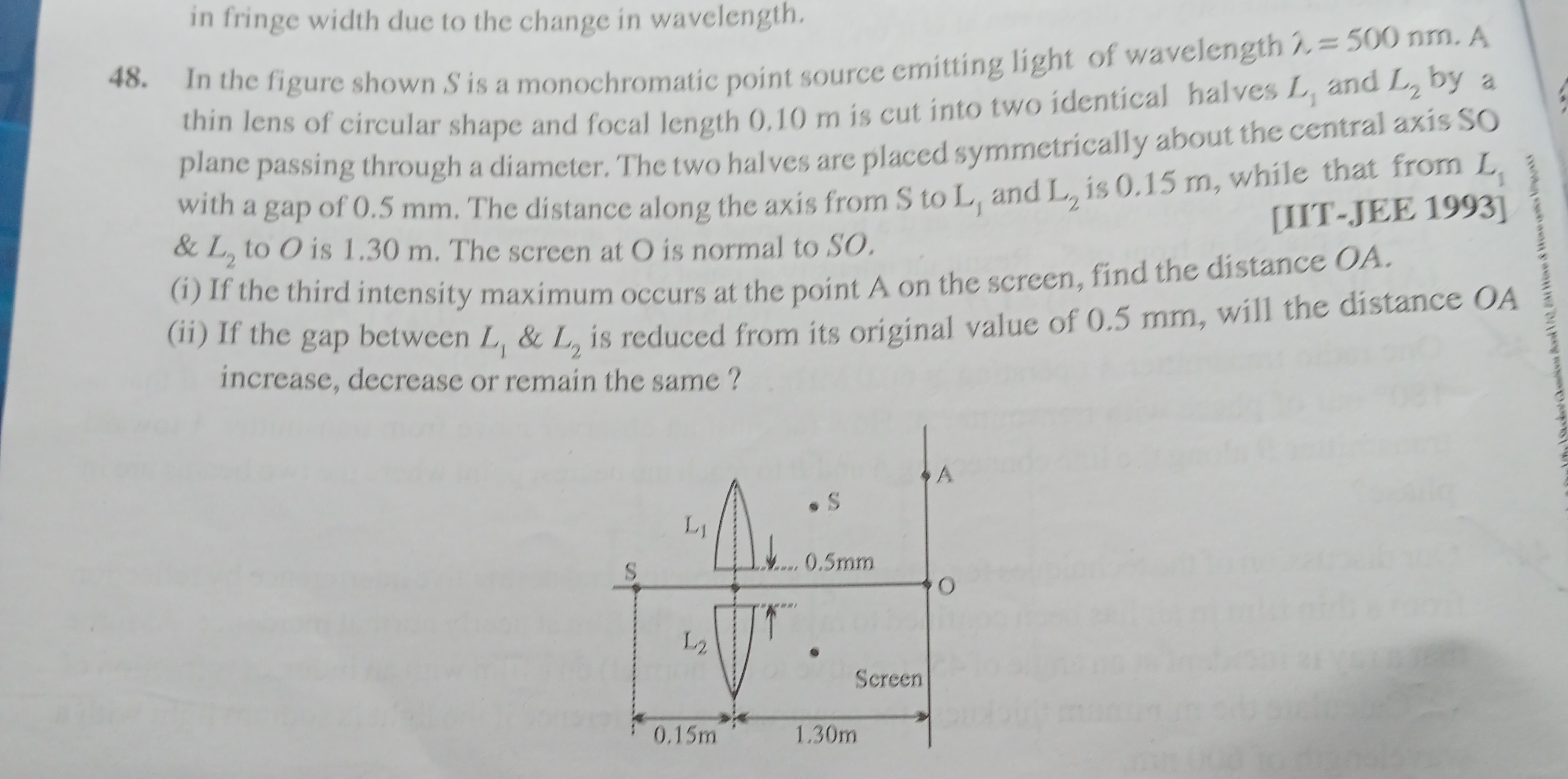
Question

In the figure shown S is a monochromatic point source emitting light of wavelength $\lambda = 500$ nm. A thin lens of circular shape and focal length 0.10 m is cut into two identical halves $L_1$ and $L_2$ by a plane passing through a diameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5 mm. The distance along the axis from S to $L_1$ and $L_2$ is 0.15 m, while that from $L_1$ & $L_2$ to O is 1.30 m. The screen at O is normal to SO. [IIT-JEE 1993]

(i) If the third intensity maximum occurs at the point A on the screen, find the distance OA.

(ii) If the gap between $L_1$ & $L_2$ is reduced from its original value of 0.5 mm, will the distance OA increase, decrease or remain the same?

Answer 1

1 mm, increase

Answer 2

The problem describes an optical setup where a point source S is placed on the axis of a lens, which is cut into two halves $L_1$ and $L_2$ separated by a gap. This arrangement creates two coherent sources, which are the images of S formed by the two lens halves. The resulting interference pattern is observed on a screen.

(i) First, we find the position of the images of the source S formed by the lens halves. The source is at a distance $u = -0.15$ m from the lens. The focal length of the lens is $f = 0.10$ m. Using the lens formula $\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$: $\frac{1}{v} = \frac{1}{f} + \frac{1}{u} = \frac{1}{0.10} + \frac{1}{-0.15} = \frac{10}{1} - \frac{100}{15} = 10 - \frac{20}{3} = \frac{30-20}{3} = \frac{10}{3}$. So, the image distance is $v = 0.30$ m. The images $S_1$ and $S_2$ are formed at a distance of 0.30 m from the lens plane.

The two lens halves are separated by a gap of 0.5 mm and placed symmetrically about the central axis SO. This means that the optical axis of $L_1$ is shifted upwards and the optical axis of $L_2$ is shifted downwards from the original axis. Let the vertical shift of the optical axis of $L_1$ be $y_0$ upwards and $L_2$ be $y_0$ downwards. The gap between the inner edges is 0.5 mm. Assuming the original lens was centered on the axis and had a diameter much larger than the gap, the optical centers of the two halves are separated by the gap plus some part of the lens. However, the problem states "with a gap of 0.5 mm". This gap is between the two halves. Let's assume the optical center of $L_1$ is at a height $y_0$ above the axis and the optical center of $L_2$ is at a depth $y_0$ below the axis, such that the separation between the optical centers is $2y_0$. The gap of 0.5 mm is the distance between the closest edges. Let's consider the effect of shifting the lens. If the lens is shifted transversely by $y_0$, the image is shifted by $y' = (1 - \frac{v}{u}) y_0$. Here $u = -0.15$ m and $v = 0.30$ m, so $\frac{v}{u} = -2$. The shift in the image is $y' = (1 - (-2)) y_0 = 3 y_0$. The problem statement and figure suggest that the gap of 0.5 mm is the separation between the two halves. A common interpretation for such a setup is that the two lens halves are obtained by cutting the lens along a diameter and then separating the two halves by a distance $d = 0.5$ mm. In this case, the two coherent sources are formed at a distance $v$ from the lens plane, and their separation is $d' = (1 - \frac{v}{u}) d$. $d' = (1 - (-2)) \times 0.5 \text{ mm} = 3 \times 0.5 \text{ mm} = 1.5$ mm.

So, we have two coherent sources $S_1$ and $S_2$ separated by a distance $d' = 1.5$ mm $= 1.5 \times 10^{-3}$ m. These sources are located at a distance of 0.30 m from the lens plane. The screen is at a distance of 1.30 m from the lens plane. The distance from the coherent sources to the screen is $D = 1.30 - 0.30 = 1.00$ m. The wavelength of light is $\lambda = 500$ nm $= 500 \times 10^{-9}$ m.

This setup is equivalent to a double-slit experiment with slit separation $d'$, screen distance $D$, and wavelength $\lambda$. The central maximum is at point O on the screen. The position of the $n$-th intensity maximum from the central maximum is given by $y_n = \frac{n \lambda D}{d'}$. We are looking for the distance OA, which is the position of the third intensity maximum, so $n=3$. $OA = y_3 = \frac{3 \lambda D}{d'} = \frac{3 \times (500 \times 10^{-9} \text{ m}) \times 1.00 \text{ m}}{1.5 \times 10^{-3} \text{ m}}$. $OA = \frac{1500 \times 10^{-9}}{1.5 \times 10^{-3}} \text{ m} = \frac{1500}{1.5} \times 10^{-6} \text{ m} = 1000 \times 10^{-6} \text{ m} = 1 \times 10^{-3} \text{ m} = 1$ mm.

(ii) If the gap between $L_1$ and $L_2$ is reduced from its original value of 0.5 mm, the separation between the two coherent sources $d'$ will also be reduced. From the formula $d' = 3d$, if $d$ decreases, then $d'$ decreases. The distance OA is given by $OA = \frac{3 \lambda D}{d'}$. Since OA is inversely proportional to $d'$, if $d'$ decreases (due to the reduction in the gap), the distance OA will increase.

The final answer is $\boxed{\text{1 mm, increase}}$.

Explanation of the solution: (i) The two lens halves form two coherent images of the source S. The distance of the images from the lens is $v=0.30$ m. The separation between the images is $d' = 3d$, where $d=0.5$ mm is the gap between the lens halves. So, $d' = 3 \times 0.5 = 1.5$ mm. The distance from the images to the screen is $D = 1.30 - 0.30 = 1.00$ m. The distance of the third maximum from the center is $y_3 = \frac{3 \lambda D}{d'} = \frac{3 \times 500 \times 10^{-9} \times 1.00}{1.5 \times 10^{-3}} = 1 \times 10^{-3}$ m $= 1$ mm. (ii) The distance OA is inversely proportional to the separation of the coherent sources $d'$. The separation $d'$ is proportional to the gap between the lens halves. If the gap is reduced, $d'$ decreases, and thus OA increases.