Question

If $y=y(x), y \in \left[0,\frac{\pi}{2}\right)$ is the solution of the differential equation $\sec y \frac{dy}{dx} - \sin(x+y) - \sin(x-y) = 0$, with

$y(0) = 0$, then $5y\left(\frac{\pi}{2}\right)$ is equal to ______.

Answer 1

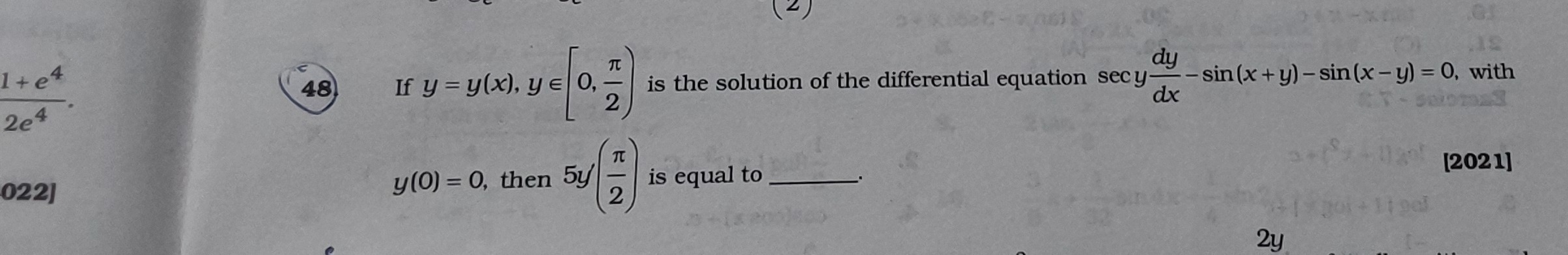
5arctan(2)

Answer 2

The given differential equation is: $\sec y \frac{dy}{dx} - \sin(x+y) - \sin(x-y) = 0$

First, simplify the trigonometric terms $\sin(x+y) + \sin(x-y)$. Using the sum-to-product identity $\sin A + \sin B = 2 \sin\left(\frac{A+B}{2}\right) \cos\left(\frac{A-B}{2}\right)$: Let $A = x+y$ and $B = x-y$. Then $\frac{A+B}{2} = \frac{(x+y) + (x-y)}{2} = \frac{2x}{2} = x$. And $\frac{A-B}{2} = \frac{(x+y) - (x-y)}{2} = \frac{2y}{2} = y$. So, $\sin(x+y) + \sin(x-y) = 2 \sin x \cos y$.

Substitute this back into the differential equation: $\sec y \frac{dy}{dx} - (2 \sin x \cos y) = 0$ $\sec y \frac{dy}{dx} = 2 \sin x \cos y$ Rewrite $\sec y$ as $\frac{1}{\cos y}$: $\frac{1}{\cos y} \frac{dy}{dx} = 2 \sin x \cos y$ Multiply both sides by $\cos y$ (note that $y \in [0, \pi/2)$, so $\cos y \neq 0$): $\frac{dy}{dx} = 2 \sin x \cos^2 y$ This is a separable differential equation. Separate the variables $y$ and $x$: $\frac{dy}{\cos^2 y} = 2 \sin x dx$ $\sec^2 y dy = 2 \sin x dx$ Now, integrate both sides: $\int \sec^2 y dy = \int 2 \sin x dx$ $\tan y = -2 \cos x + C$ Use the initial condition $y(0) = 0$ to find the constant $C$: Substitute $x=0$ and $y=0$ into the general solution: $\tan(0) = -2 \cos(0) + C$ $0 = -2(1) + C$ $C = 2$ So, the particular solution to the differential equation is: $\tan y = -2 \cos x + 2$ $\tan y = 2(1 - \cos x)$ We need to find the value of $5y\left(\frac{\pi}{2}\right)$. First, find $y\left(\frac{\pi}{2}\right)$ by substituting $x = \frac{\pi}{2}$ into the solution: $\tan\left(y\left(\frac{\pi}{2}\right)\right) = 2\left(1 - \cos\left(\frac{\pi}{2}\right)\right)$ Since $\cos\left(\frac{\pi}{2}\right) = 0$: $\tan\left(y\left(\frac{\pi}{2}\right)\right) = 2(1 - 0)$ $\tan\left(y\left(\frac{\pi}{2}\right)\right) = 2$ Let $y_0 = y\left(\frac{\pi}{2}\right)$. Then $\tan y_0 = 2$. Since $y \in \left[0,\frac{\pi}{2}\right)$, $y_0$ must be $\arctan(2)$. So, $y\left(\frac{\pi}{2}\right) = \arctan(2)$. The question asks for $5y\left(\frac{\pi}{2}\right)$: $5y\left(\frac{\pi}{2}\right) = 5 \arctan(2)$

Thus, the final answer is $5\arctan(2)$.