Solveeit Logo
Login

Question

Question: If $\sin^{-1}x + \cos^{-1}y = \frac{3\pi}{10}$, then the value of $\cos^{-1}x + \sin^{-1}y$ is...

If sin⁡−1x+cos⁡−1y=3π10\sin^{-1}x + \cos^{-1}y = \frac{3\pi}{10}, then the value of cos⁡−1x+sin⁡−1y\cos^{-1}x + \sin^{-1}y is

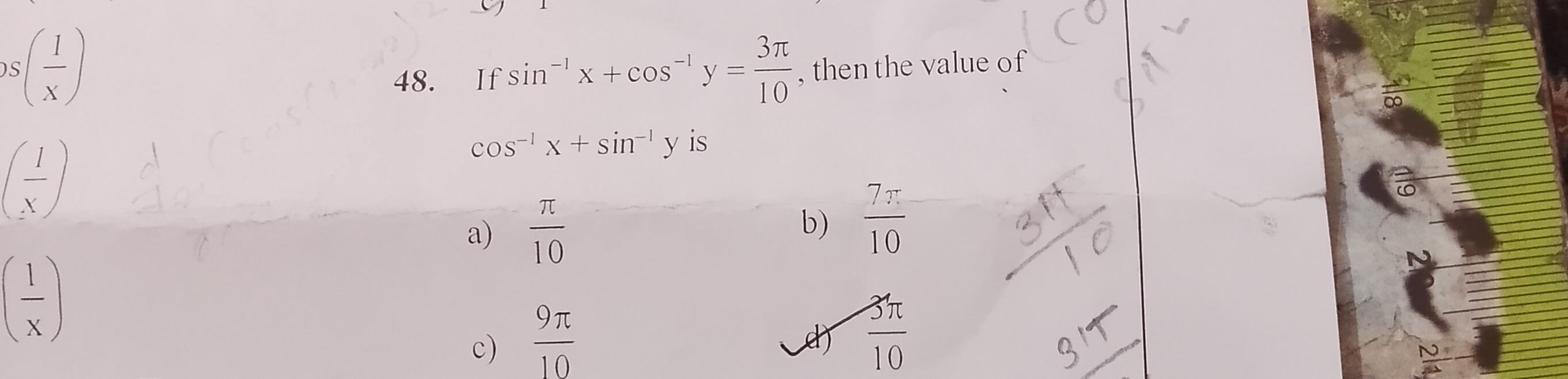
A

π10\frac{\pi}{10}

B

7π10\frac{7\pi}{10}

C

9π10\frac{9\pi}{10}

D

3π10\frac{3\pi}{10}

Answer

7π10\dfrac{7\pi}{10}

Explanation

Solution

Explanation:
Let

A=sin⁡−1xandB=cos⁡−1y.A = \sin^{-1}x \quad \text{and} \quad B = \cos^{-1}y.

We are given A+B=3π10A + B = \dfrac{3\pi}{10}.
Recall that:

cos⁡−1x=π2−sin⁡−1xandsin⁡−1y=π2−cos⁡−1y.\cos^{-1}x = \frac{\pi}{2} - \sin^{-1}x \quad \text{and} \quad \sin^{-1}y = \frac{\pi}{2} - \cos^{-1}y.

Thus,

cos⁡−1x+sin⁡−1y=(π2−A)+(π2−B)=π−(A+B)=π−3π10=7π10.\cos^{-1}x + \sin^{-1}y = \left(\frac{\pi}{2} - A\right) + \left(\frac{\pi}{2} - B\right) = \pi - (A+B) = \pi - \frac{3\pi}{10} = \frac{7\pi}{10}.