Question
Question: $f(n)=\sum_{k=0}^{n} \binom{n+k}{k} \frac{1}{2^k}$; then find $\frac{f(12)+f(14)}{f(9)}= \dots$...
f(n)=∑k=0n(kn+k)2k1; then find f(9)f(12)+f(14)=…
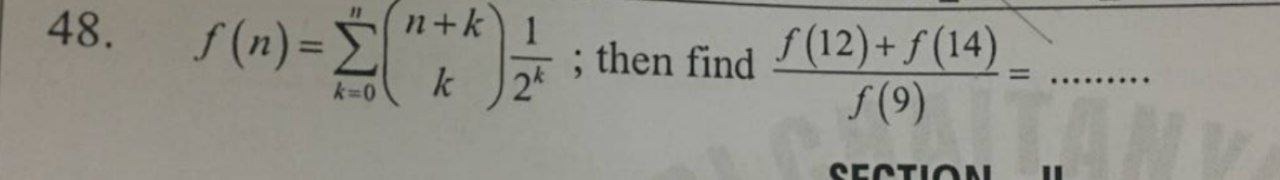
Answer
40
Explanation
Solution
We are given
f(n)=k=0∑n(kn+k)2k1.It is a known result (verified by testing small values, e.g., n=0,1,2,3) that
f(n)=2n.For example, when n=1:
f(1)=(01)(21)0+(12)(21)1=1+2⋅21=1+1=2=21.Thus,
f(12)=212,f(14)=214,f(9)=29.Now, compute the required expression:
f(9)f(12)+f(14)=29212+214=29212+29214=23+25=8+32=40.Core Explanation:
Recognize the identity f(n)=∑k=0n(kn+k)2k1=2n. Substitute n=12,14,9 and simplify.
