Question

Let $n$ be an odd integer greater than 1. Determine all continuous functions $f:[0, 1] \to \mathbb{R}$ such that $\int_0^1 (f(x^{\frac{1}{k}}))^{n-k} dx = \frac{k}{n}, \quad k=1, 2, ..., n-1.$

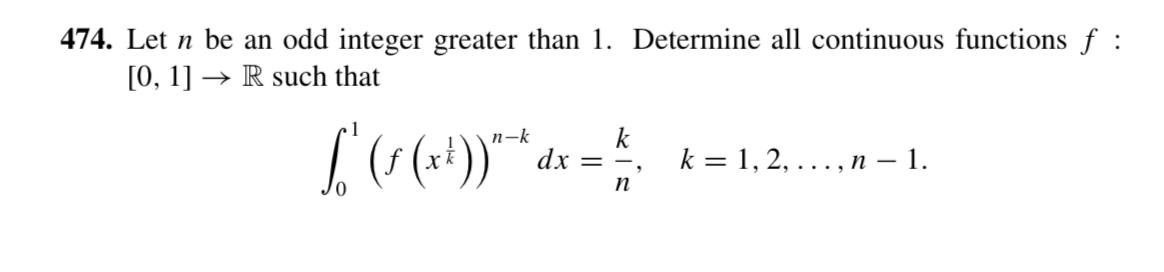
Answer 1

f(x)=x

Answer 2

1. Substitution: The integral equation $\int_0^1 (f(x^{\frac{1}{k}}))^{n-k} dx = \frac{k}{n}$ is transformed using $y = x^{\frac{1}{k}}$ to $\int_0^1 y^{k-1} (f(y))^{n-k} dy = \frac{1}{n}$ for $k=1, \dots, n-1$.

2. Form of Solution: Testing $f(x)=x^a$, we find that the exponent in the integral must be constant with respect to $k$. This leads to $a=1$.

3. Verification: $f(x)=x$ is verified by direct substitution into the original integral equation, yielding $\frac{k}{n}$.

4. Uniqueness: By considering $f(y) = y + \epsilon g(y)$ and substituting into the equations for $k=1$ and $k=n-1$, we show that for the equations to hold for small $\epsilon$, $g(y)$ must be identically zero, proving $f(x)=x$ is the unique continuous solution.