Question
Question: The value of $\lim_{n \to \infty} (\frac{n!}{n^n})^{\frac{3n^3+4}{4n^4-1}}$, $n \in N$ is equal to :...
The value of limn→∞(nnn!)4n4−13n3+4, n∈N is equal to :
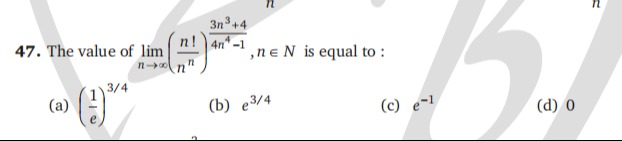
(e1)3/4
e3/4
e−1
0
(e1)3/4
Solution
Let the given limit be L. The expression is L=limn→∞(nnn!)4n4−13n3+4.
This is of the form limn→∞(an)bn, where an=nnn! and bn=4n4−13n3+4.
First, let's find the limit of the base an: an=nnn!=n⋅n⋅n⋯n1⋅2⋅3⋯n=n1⋅n2⋅n3⋯nn.
For n>1, nk≤1 for all k=1,2,…,n. So, 0<an=n1⋅n2⋯nn≤n1⋅1⋯1=n1. As n→∞, n1→0. By the Squeeze Theorem, limn→∞an=0.
Next, let's find the limit of the exponent bn: bn=4n4−13n3+4. To find the limit as n→∞, we divide the numerator and the denominator by the highest power of n in the denominator, which is n4:
limn→∞bn=limn→∞n44n4−n41n43n3+n44=limn→∞4−n41n3+n44=4−00+0=0.
The limit is of the indeterminate form 00. To evaluate this limit, we consider the limit of the logarithm of the expression:
lnL=limn→∞ln[(nnn!)4n4−13n3+4]=limn→∞(4n4−13n3+4)ln(nnn!).
Let's evaluate the limit of the term ln(nnn!). ln(nnn!)=ln(n!)−ln(nn)=ln(n!)−nlnn.
We use the approximation for ln(n!) for large n from Stirling's formula: ln(n!)=nlnn−n+21ln(2πn)+O(n1).
So, ln(nnn!)=(nlnn−n+21ln(2πn)+O(n1))−nlnn=−n+21ln(2πn)+O(n1).
Now, substitute this back into the limit of lnL: lnL=limn→∞(4n4−13n3+4)(−n+21ln(2πn)+O(n1)).
Let's multiply the leading terms: limn→∞(4n43n3)(−n)=limn→∞(4n3)(−n)=limn→∞−43=−43.
Let's verify that the other terms go to zero. The expression is 4n4−13n3+4=n4(4−1/n4)n3(3+4/n3)=n14−1/n43+4/n3. The term ln(nnn!)=−n+21ln(2πn)+O(n1).
The product is (n14−1/n43+4/n3)(−n+21ln(2πn)+O(n1)) =4−1/n43+4/n3⋅n1(−n+21ln(2πn)+O(n1)) =4−1/n43+4/n3⋅(−1+2nln(2πn)+O(n21)).
As n→∞: 4−1/n43+4/n3→4−03+0=43. 2nln(2πn)→0 (since lnx grows slower than x). O(n21)→0.
So, limn→∞lnL=43⋅(−1+0+0)=−43. Therefore, lnL=−43. L=e−3/4. This can also be written as L=(e−1)3/4=(e1)3/4.
Our result matches option (a).
