Question
Question: The value of $\cos^{-1}\left[\cos \left(\frac{\pi}{2}\right)\right]+\cos^{-1}\left[\sin \left(\frac{...
The value of cos−1[cos(2π)]+cos−1[sin(32π)] is
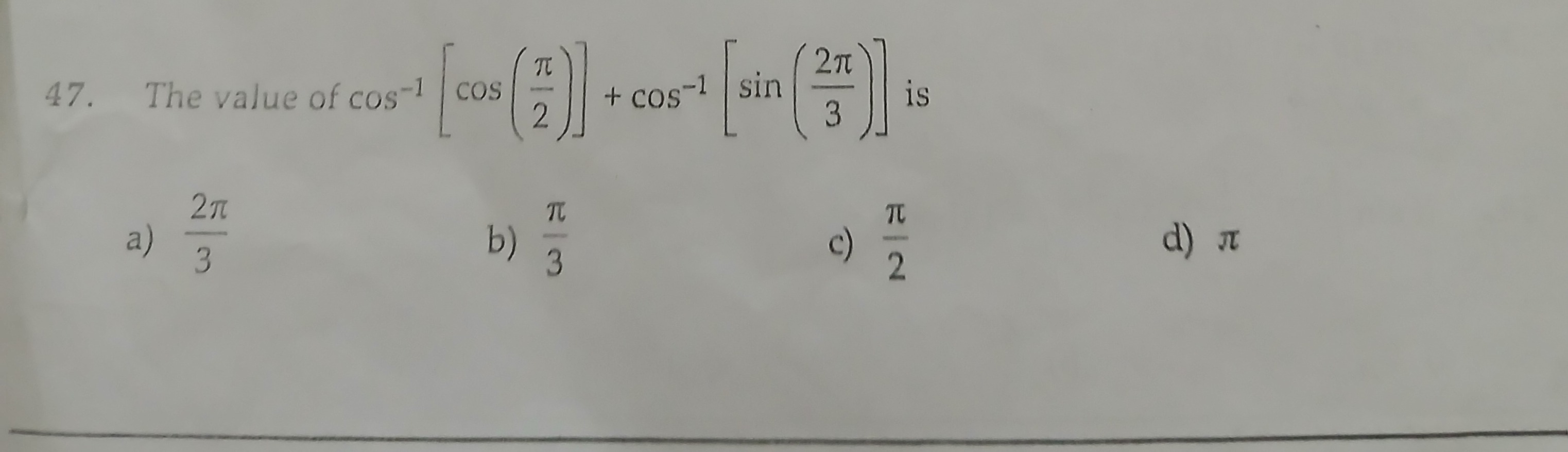
A
32π
B
3π
C
2π
D
π
Answer
32π
Explanation
Solution
-
Evaluate cos−1(cos(π/2)).
Since π/2 lies in the principal range [0,π] for cos−1, we have:
cos−1(cos(π/2))=π/2. -
Evaluate cos−1(sin(2π/3)).
Note that:
sin(2π/3)=sin(π−π/3)=sin(π/3)=3/2.Since cos(π/6)=3/2 and π/6 is in [0,π], we get:
cos−1(3/2)=π/6. -
Sum the results:
π/2+π/6=63π+6π=64π=32π.
