Question

The ratio of maximum to minimum wavelength in Balmer series of hydrogen atom is .......

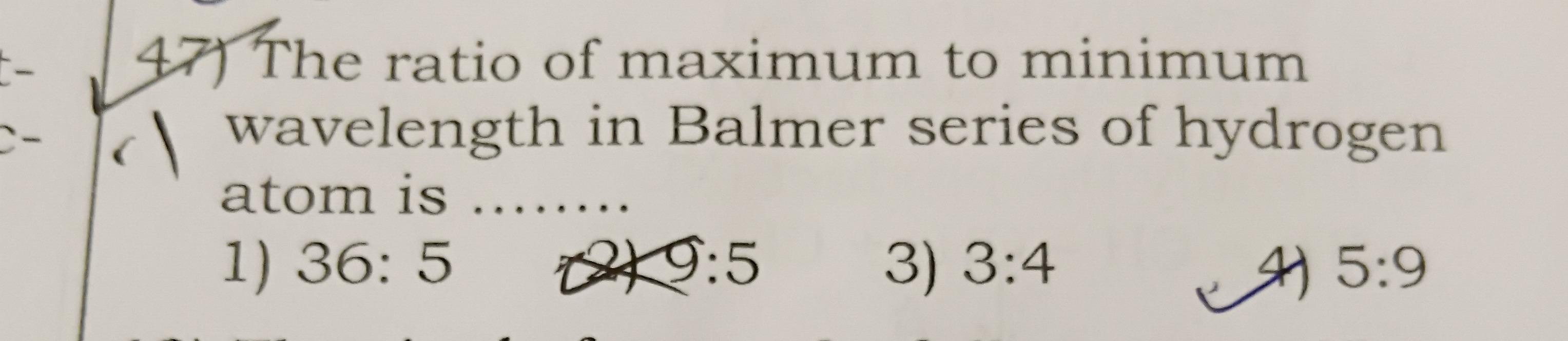
• A. 36: 5
• B. 9:5
• C. 3:4
• D. 5:9

Answer 1

Answer: (B)

9:5

Answer 2

For the Balmer series, the wavelength is given by

$$\frac{1}{\lambda} = R\left(\frac{1}{2^2} - \frac{1}{n^2}\right)$$

• The shortest wavelength (minimum wavelength, $\lambda_{\min}$) occurs for $n=\infty$: $$\frac{1}{\lambda_{\min}}= R\left(\frac{1}{4}-0\right)=\frac{R}{4}.$$
• The longest wavelength (maximum wavelength, $\lambda_{\max}$) occurs for $n=3$: $$\frac{1}{\lambda_{\max}} = R\left(\frac{1}{4} - \frac{1}{9}\right)= R\left(\frac{9-4}{36}\right)=\frac{5R}{36}.$$

Thus,

$$\lambda_{\min} = \frac{4}{R}, \quad \lambda_{\max} = \frac{36}{5R}.$$

The ratio of maximum to minimum wavelength is:

$$\frac{\lambda_{\max}}{\lambda_{\min}} = \frac{\frac{36}{5R}}{\frac{4}{R}} = \frac{36}{5}\times\frac{R}{4}\times\frac{1}{R} = \frac{36}{20} = \frac{9}{5}.$$