Solveeit Logo
Login

Question

Question: If $x = \frac{1}{1^2} + \frac{1}{3^2} + \frac{1}{5^2} + ..., y = \frac{1}{1^2} + \frac{3}{2^2} + \fr...

If x=112+132+152+...,y=112+322+132+342+...x = \frac{1}{1^2} + \frac{1}{3^2} + \frac{1}{5^2} + ..., y = \frac{1}{1^2} + \frac{3}{2^2} + \frac{1}{3^2} + \frac{3}{4^2} + ... and z=112−122+132−142+...z = \frac{1}{1^2} - \frac{1}{2^2} + \frac{1}{3^2} - \frac{1}{4^2} + ... then

A

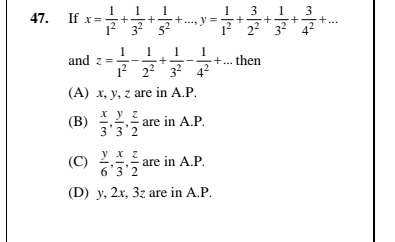
x,y,zx, y, z are in A.P.

B

x3,y3,z2\frac{x}{3}, \frac{y}{3}, \frac{z}{2} are in A.P.

C

y6,x3,z2\frac{y}{6}, \frac{x}{3}, \frac{z}{2} are in A.P.

D

y,2x,3zy, 2x, 3z are in A.P.

Answer

Options (C) and (D) are correct. In option (C), y6=x3=z2=π224\frac{y}{6} = \frac{x}{3} = \frac{z}{2} = \frac{\pi^2}{24}, so they are in A.P. In option (D), y=2x=3z=π24y = 2x = 3z = \frac{\pi^2}{4}, so they are in A.P.

Explanation

Solution

Here's how to solve this problem:

  1. Define S=∑n=1∞1n2=π26S = \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}.

  2. Express xx in terms of SS: x=∑n=1∞1(2n−1)2=S−∑n=1∞1(2n)2=S−14S=34S=34π26=π28x = \sum_{n=1}^{\infty} \frac{1}{(2n-1)^2} = S - \sum_{n=1}^{\infty} \frac{1}{(2n)^2} = S - \frac{1}{4}S = \frac{3}{4}S = \frac{3}{4} \frac{\pi^2}{6} = \frac{\pi^2}{8}.

  3. Express yy in terms of xx and SS: y=∑n=1∞1(2n−1)2+∑n=1∞3(2n)2=x+34S=π28+34π26=π28+π28=π24y = \sum_{n=1}^{\infty} \frac{1}{(2n-1)^2} + \sum_{n=1}^{\infty} \frac{3}{(2n)^2} = x + \frac{3}{4}S = \frac{\pi^2}{8} + \frac{3}{4} \frac{\pi^2}{6} = \frac{\pi^2}{8} + \frac{\pi^2}{8} = \frac{\pi^2}{4}.

  4. Express zz in terms of xx and SS: z=∑n=1∞(−1)n+1n2=∑n=1∞1(2n−1)2−∑n=1∞1(2n)2=x−14S=π28−14π26=π28−π224=2π224=π212z = \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n^2} = \sum_{n=1}^{\infty} \frac{1}{(2n-1)^2} - \sum_{n=1}^{\infty} \frac{1}{(2n)^2} = x - \frac{1}{4}S = \frac{\pi^2}{8} - \frac{1}{4} \frac{\pi^2}{6} = \frac{\pi^2}{8} - \frac{\pi^2}{24} = \frac{2\pi^2}{24} = \frac{\pi^2}{12}.

  5. Check options for A.P. condition (2b=a+c2b = a+c):

    • (C) y6,x3,z2\frac{y}{6}, \frac{x}{3}, \frac{z}{2}: y6=π2/46=π224\frac{y}{6} = \frac{\pi^2/4}{6} = \frac{\pi^2}{24} x3=π2/83=π224\frac{x}{3} = \frac{\pi^2/8}{3} = \frac{\pi^2}{24} z2=π2/122=π224\frac{z}{2} = \frac{\pi^2/12}{2} = \frac{\pi^2}{24} Since all terms are equal, they are in A.P. (common difference 0).

    • (D) y,2x,3zy, 2x, 3z: y=π24y = \frac{\pi^2}{4} 2x=2(π28)=π242x = 2(\frac{\pi^2}{8}) = \frac{\pi^2}{4} 3z=3(π212)=π243z = 3(\frac{\pi^2}{12}) = \frac{\pi^2}{4} Since all terms are equal, they are in A.P. (common difference 0).

Both (C) and (D) are correct options.