Question

If a, b, c are side of triangle ABC and $a^3$, $b^3$, $c^3$ are roots of $x^3 - px^2 + qx - r = 0$ where $p, q, r \in N$ and $\sin^3 A + \sin^3 B + \sin^3 C - 3 \sin A \sin B \sin C = 8\Delta^3$. (Where $\Delta$ is area of triangle ABC) then find minimum value of (p + r)_____

Answer 1

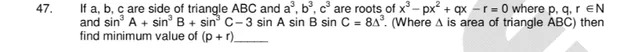
5

Answer 2

The problem asks for the minimum value of $(p+r)$ given certain conditions about a triangle ABC and a cubic equation.

1. Analyze the given condition involving $\sin A, \sin B, \sin C$ and $\Delta$: The given condition is $\sin^3 A + \sin^3 B + \sin^3 C - 3 \sin A \sin B \sin C = 8\Delta^3$. We use the Sine Rule: $\sin A = \frac{a}{2R}$, $\sin B = \frac{b}{2R}$, $\sin C = \frac{c}{2R}$, where R is the circumradius. Substitute these into the equation: $\frac{a^3}{(2R)^3} + \frac{b^3}{(2R)^3} + \frac{c^3}{(2R)^3} - 3 \frac{a}{2R} \frac{b}{2R} \frac{c}{2R} = 8\Delta^3$ $\frac{1}{8R^3} (a^3 + b^3 + c^3 - 3abc) = 8\Delta^3$ $a^3 + b^3 + c^3 - 3abc = 64R^3\Delta^3$ We know the formula for the area of a triangle: $\Delta = \frac{abc}{4R}$. From this, we can write $abc = 4R\Delta$. Substitute $abc = 4R\Delta$ into the right side of the equation: $64R^3\Delta^3 = 64 (R\Delta)^3 = 64 \left(\frac{abc}{4}\right)^3 = 64 \frac{a^3b^3c^3}{64} = a^3b^3c^3$ So, the given condition simplifies to: $a^3 + b^3 + c^3 - 3abc = a^3b^3c^3 \quad (*)$

2. Relate the cubic equation roots to $p, q, r$: The roots of the cubic equation $x^3 - px^2 + qx - r = 0$ are $a^3, b^3, c^3$. Using Vieta's formulas: Sum of roots: $a^3+b^3+c^3 = p$ Product of roots: $a^3b^3c^3 = r$

3. Substitute $p$ and $r$ into equation $(*)$: From equation $(*)$, we have: $p - 3abc = r$ We also know $abc = \sqrt[3]{r}$. So, $p - 3\sqrt[3]{r} = r$. This implies $p = r + 3\sqrt[3]{r}$.

4. Express $(p+r)$ in terms of $r$: We need to find the minimum value of $(p+r)$. Substitute the expression for $p$: $p+r = (r + 3\sqrt[3]{r}) + r = 2r + 3\sqrt[3]{r}$.

5. Determine the constraints on $r$: The problem states that $p, q, r \in N$ (natural numbers), which means $p, q, r \ge 1$. Since $r = a^3b^3c^3$, and $a, b, c$ are sides of a triangle (positive real numbers), $r$ must be a positive real number. Since $r$ must be a natural number, the smallest possible value for $r$ is 1.

6. Find the minimum value of $(p+r)$: Let $f(r) = 2r + 3\sqrt[3]{r}$. To find the minimum value of $f(r)$ for $r \in N$, we check the smallest natural number value for $r$. If $r=1$: $p+r = 2(1) + 3\sqrt[3]{1} = 2 + 3 = 5$.

7. Check if $r=1$ is achievable and valid: If $r=1$, then $a^3b^3c^3 = 1$, which implies $abc=1$. From $p = r + 3\sqrt[3]{r}$, if $r=1$, then $p = 1 + 3\sqrt[3]{1} = 1+3=4$. Both $p=4$ and $r=1$ are natural numbers. Now we need to check if a triangle exists such that $abc=1$ and the condition $a^3+b^3+c^3-3abc = a^3b^3c^3$ holds. If $abc=1$, the condition becomes $a^3+b^3+c^3-3(1) = 1$. So $a^3+b^3+c^3 = 4$. This is consistent with $p=4$. We also need $q = a^3b^3+b^3c^3+c^3a^3$ to be a natural number. If $abc=1$, then $q = \frac{1}{c^3} + \frac{1}{a^3} + \frac{1}{b^3}$. Consider the case where $a=1, b=1, c=1$. This forms an equilateral triangle with side length 1. For this triangle: $abc = 1 \cdot 1 \cdot 1 = 1$. This satisfies $abc=1$. $a^3=1, b^3=1, c^3=1$. $p = a^3+b^3+c^3 = 1+1+1=3$. $q = a^3b^3+b^3c^3+c^3a^3 = 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 = 3$. $r = a^3b^3c^3 = 1 \cdot 1 \cdot 1 = 1$. All $p=3, q=3, r=1$ are natural numbers. However, for $a=b=c=1$, the condition $a^3+b^3+c^3-3abc = a^3b^3c^3$ becomes $1+1+1-3(1)(1)(1) = (1)(1)(1)$, which simplifies to $0=1$. This is false. Therefore, $a=b=c=1$ is not a valid triangle for this problem.

This means that $p=4, r=1$ (derived from $abc=1$) is not achievable through $a=b=c=1$. The function $f(r) = 2r + 3r^{1/3}$ is an increasing function for $r > 0$. Its derivative $f'(r) = 2 + r^{-2/3} > 0$ for all $r>0$. Since $r$ must be a natural number, the minimum value of $f(r)$ will occur at the smallest possible natural number value for $r$, which is $r=1$. The fact that $a=b=c=1$ does not satisfy the original condition does not mean that $r=1$ is unachievable. It just means that $a=b=c=1$ is not the triangle. We need to find if there exists any triangle $(a,b,c)$ such that $a^3b^3c^3=1$ and $a^3+b^3+c^3-3abc = a^3b^3c^3$. As shown, these conditions imply $a^3+b^3+c^3=4$ and $abc=1$. We also need $q = a^3b^3+b^3c^3+c^3a^3$ to be a natural number. Let $a^3=x, b^3=y, c^3=z$. We need $x+y+z=4$, $xyz=1$, and $xy+yz+zx$ to be a natural number. Consider $x=1/2, y=1/2, z=2$. Then $x+y+z=1/2+1/2+2=3 \ne 4$. Consider $x=1, y=1, z=2$. Then $x+y+z=4$, $xyz=2 \ne 1$. Consider $x=1/2, y=1, z=2$. $xyz=1$. $x+y+z=1/2+1+2=3.5 \ne 4$. Consider $x=1/3, y=1, z=3$. $xyz=1$. $x+y+z=1/3+1+3=13/3 \ne 4$. Consider $x=1/4, y=1, z=4$. $xyz=1$. $x+y+z=1/4+1+4=21/4 \ne 4$. Consider $x=1/k, y=k, z=1$. $xyz=1$. $x+y+z=1/k+k+1=4$. $k^2+k+1 = 4k \implies k^2-3k+1=0$. $k = \frac{3 \pm \sqrt{9-4}}{2} = \frac{3 \pm \sqrt{5}}{2}$. Let $k = \frac{3+\sqrt{5}}{2}$. Then $x = \frac{2}{3+\sqrt{5}} = \frac{2(3-\sqrt{5})}{9-5} = \frac{3-\sqrt{5}}{2}$. So, $a^3 = \frac{3-\sqrt{5}}{2}$, $b^3 = \frac{3+\sqrt{5}}{2}$, $c^3 = 1$. Are $a,b,c$ sides of a triangle? $a = \left(\frac{3-\sqrt{5}}{2}\right)^{1/3}$, $b = \left(\frac{3+\sqrt{5}}{2}\right)^{1/3}$, $c = 1$. We need to check triangle inequality: $a+b>c$, $b+c>a$, $c+a>b$. Let's check $q = a^3b^3+b^3c^3+c^3a^3 = xy+yz+zx$. $q = \frac{3-\sqrt{5}}{2} \cdot \frac{3+\sqrt{5}}{2} + \frac{3+\sqrt{5}}{2} \cdot 1 + 1 \cdot \frac{3-\sqrt{5}}{2}$ $q = \frac{9-5}{4} + \frac{3+\sqrt{5}}{2} + \frac{3-\sqrt{5}}{2}$ $q = \frac{4}{4} + \frac{3+\sqrt{5}+3-\sqrt{5}}{2} = 1 + \frac{6}{2} = 1+3=4$. So, $q=4$, which is a natural number. So, we have $p=4, q=4, r=1$. All are natural numbers. The cubic equation is $x^3-4x^2+4x-1=0$. The roots are $a^3, b^3, c^3$. We have $a^3 = \frac{3-\sqrt{5}}{2}$, $b^3 = \frac{3+\sqrt{5}}{2}$, $c^3 = 1$. We need to verify if $a, b, c$ form a triangle. $a = \left(\frac{3-\sqrt{5}}{2}\right)^{1/3} \approx (0.38)^{1/3} \approx 0.72$ $b = \left(\frac{3+\sqrt{5}}{2}\right)^{1/3} \approx (2.618)^{1/3} \approx 1.37$ $c = 1$. Check triangle inequality: $a+b \approx 0.72+1.37 = 2.09 > 1$ (c) - True $a+c \approx 0.72+1 = 1.72 > 1.37$ (b) - True $b+c \approx 1.37+1 = 2.37 > 0.72$ (a) - True Since all triangle inequalities hold, such a triangle exists. Thus, $r=1$ is an achievable value, and it gives the minimum value for $p+r$.

Minimum value of $(p+r) = 5$.