Question
Question: The value of the definite integral $\int_{0}^{\frac{\pi}{2}} (\cos^{10}x \cdot \sin 12x) dx$, is equ...
The value of the definite integral ∫02π(cos10x⋅sin12x)dx, is equal to
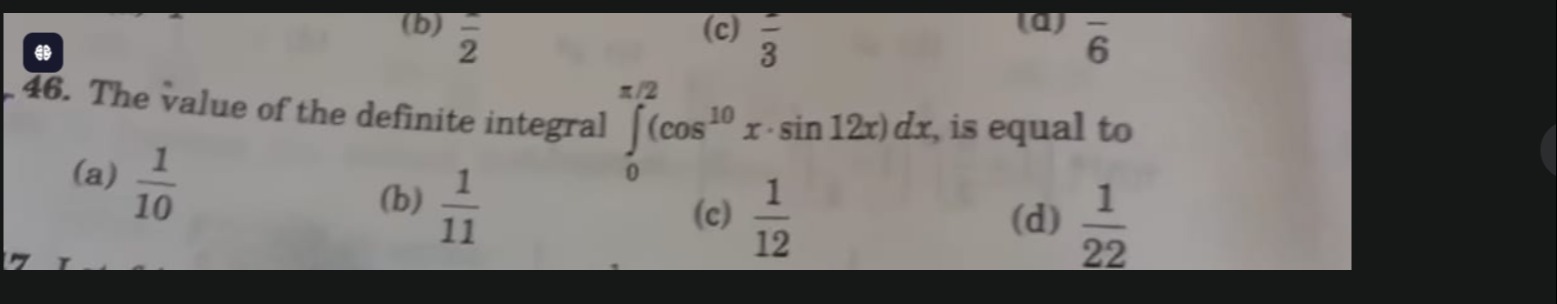
1/10
1/11
1/12
1/22
1/11
Solution
The problem asks for the value of the definite integral I=∫02π(cos10x⋅sin12x)dx. The integral is of the form ∫02πcosmxsinnxdx. For this type of integral, the Wallis' integral formula states: ∫02πcosmxsinnxdx={(m+n)!!(m−1)!!(n−1)!!(m+n)!!(m−1)!!(n−1)!!2πif m+n is oddif m and n are both even In the given problem, m=10 and n=12. Both m and n are even, and m+n=22 is also even. According to the formula, the integral should be: I=(10+12)!!(10−1)!!(12−1)!!2π=22!!9!!⋅11!!2π This result involves π, but the given options are simple fractions without π. This strongly suggests a typo in the question. A common scenario is that one of the powers was intended to be 1, leading to an odd sum of powers.
Let's assume there was a typo and the integral was intended to be ∫02π(cos10x⋅sin1x)dx. In this case, m=10 and n=1. The sum of the powers is m+n=10+1=11, which is odd. Using the Wallis' integral formula for an odd sum of powers: I=(m+n)!!(m−1)!!(n−1)!! Substituting m=10 and n=1: I=(10+1)!!(10−1)!!(1−1)!!=11!!9!!⋅0!! By convention, 0!!=1. I=11!!9!! The double factorial k!! is the product of all integers from k down to 1 with the same parity as k. 9!!=9×7×5×3×1 11!!=11×9×7×5×3×1 Therefore, I=11×9×7×5×3×19×7×5×3×1=111 This result matches option (b). Given the discrepancy between the calculated value for the original question (which includes π) and the provided options, it is reasonable to conclude that the question likely contained a typo and was intended to be ∫02π(cos10x⋅sin1x)dx, yielding the answer 111.
