Solveeit Logo
Login

Question

Question: The value of $\tan^{-1}\left\{ \frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right\}+\frac{1}{...

The value of tan⁡−1{1+x−1−x1+x+1−x}+12cos⁡−1x\tan^{-1}\left\{ \frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right\}+\frac{1}{2}\cos^{-1}x is

[2024]

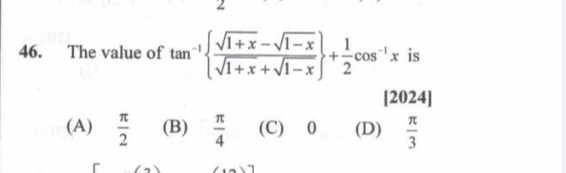
A

π2\frac{\pi}{2}

B

π4\frac{\pi}{4}

C

0

D

π3\frac{\pi}{3}

Answer

π4\frac{\pi}{4}

Explanation

Solution

Let x=cos⁡θx = \cos\theta, where θ∈[0,π]\theta \in [0, \pi]. Then,

1+x=1+cos⁡θ=2cos⁡θ2,1−x=1−cos⁡θ=2sin⁡θ2.\sqrt{1+x} = \sqrt{1+\cos\theta} = \sqrt{2}\cos\frac{\theta}{2},\quad \sqrt{1-x} = \sqrt{1-\cos\theta} = \sqrt{2}\sin\frac{\theta}{2}.

Thus, the fraction becomes:

1+x−1−x1+x+1−x=cos⁡θ2−sin⁡θ2cos⁡θ2+sin⁡θ2.\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}} = \frac{\cos\frac{\theta}{2}-\sin\frac{\theta}{2}}{\cos\frac{\theta}{2}+\sin\frac{\theta}{2}}.

Notice that:

tan⁡(π4−θ2)=1−tan⁡θ21+tan⁡θ2=cos⁡θ2−sin⁡θ2cos⁡θ2+sin⁡θ2.\tan\left(\frac{\pi}{4} - \frac{\theta}{2}\right) = \frac{1 - \tan\frac{\theta}{2}}{1 + \tan\frac{\theta}{2}} = \frac{\cos\frac{\theta}{2}-\sin\frac{\theta}{2}}{\cos\frac{\theta}{2}+\sin\frac{\theta}{2}}.

Thus,

tan⁡−1(1+x−1−x1+x+1−x)=π4−θ2.\tan^{-1}\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right) = \frac{\pi}{4} - \frac{\theta}{2}.

Also, since x=cos⁡θx = \cos\theta, we have:

cos⁡−1x=θ.\cos^{-1}x = \theta.

Therefore, the given expression simplifies to:

(π4−θ2)+12θ=π4.\left(\frac{\pi}{4} - \frac{\theta}{2}\right) + \frac{1}{2}\theta = \frac{\pi}{4}.