Question

$\sum_{n=3}^{\infty} \frac{2^{n^2}}{n^{2^n}}$

Answer 1

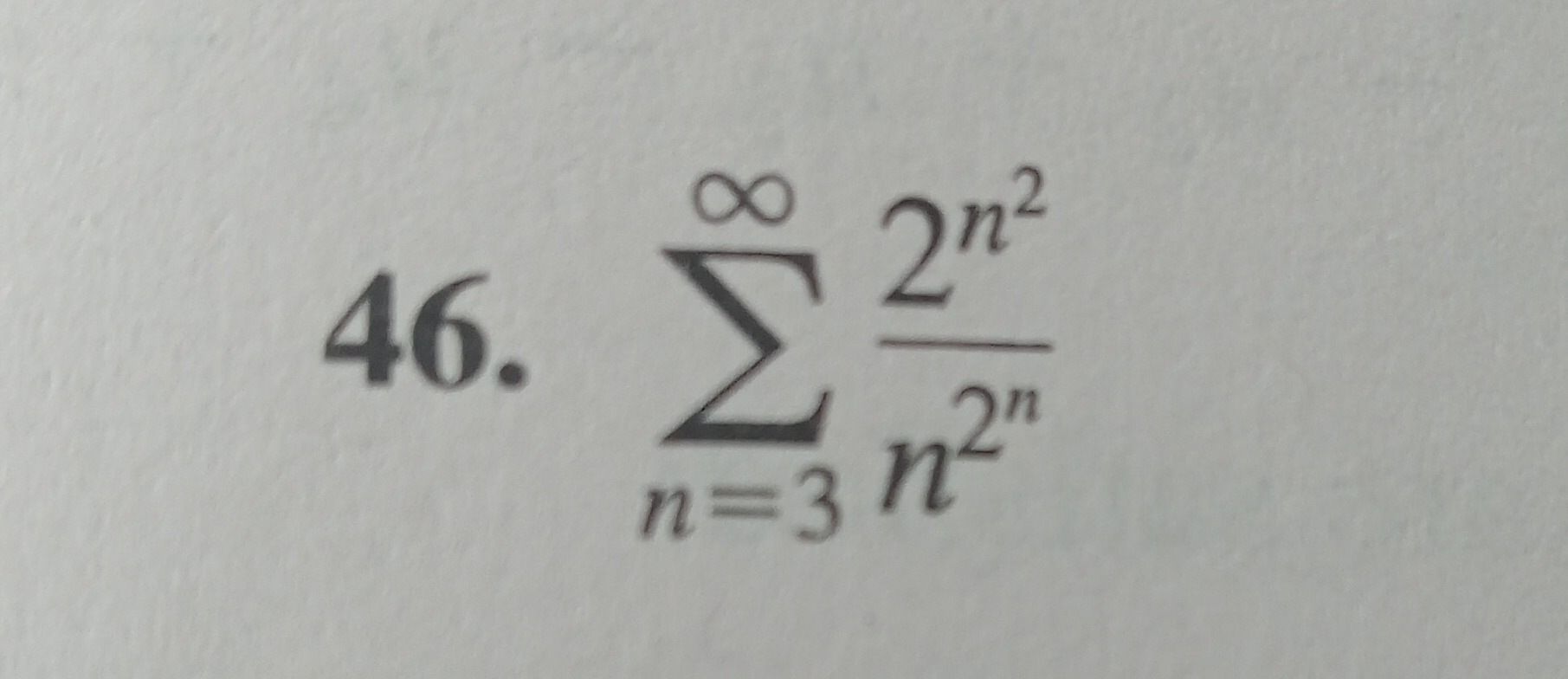
The sum of the series cannot be determined using standard JEE/NEET techniques. The terms are positive, so the sum is not 0. If the question is from a context where such complex sums are not expected to be evaluated, or if it's a trick question with a flawed premise, the answer might be intended as 0.

Answer 2

The problem asks for the sum of the series $\sum_{n=3}^{\infty} \frac{2^{n^2}}{n^{2^n}}$. Let the general term be $a_n = \frac{2^{n^2}}{n^{2^n}}$.

We first check for convergence using the Root Test: $|a_n|^{1/n} = \left( \frac{2^{n^2}}{n^{2^n}} \right)^{1/n} = \frac{(2^{n^2})^{1/n}}{(n^{2^n})^{1/n}} = \frac{2^{n^2 \cdot \frac{1}{n}}}{n^{2^n \cdot \frac{1}{n}}} = \frac{2^n}{n^{2^{n-1}}}$.

Now, we evaluate the limit $L = \lim_{n \to \infty} \frac{2^n}{n^{2^{n-1}}}$. To assess this limit, consider the growth rates. The denominator $n^{2^{n-1}}$ grows significantly faster than the numerator $2^n$. Let's examine the logarithm of the term: $\ln\left(\frac{2^n}{n^{2^{n-1}}}\right) = \ln(2^n) - \ln(n^{2^{n-1}}) = n \ln(2) - 2^{n-1} \ln(n)$. As $n \to \infty$, the term $2^{n-1} \ln(n)$ grows much faster than $n \ln(2)$. Thus, $\lim_{n \to \infty} (n \ln(2) - 2^{n-1} \ln(n)) = -\infty$. Therefore, $L = \lim_{n \to \infty} \frac{2^n}{n^{2^{n-1}}} = e^{-\infty} = 0$. Since $L=0 < 1$, the series converges by the Root Test.

However, the question asks for the sum of the series. The terms $a_n = \frac{2^{n^2}}{n^{2^n}}$ are positive for $n \ge 3$. For instance: $a_3 = \frac{2^{3^2}}{3^{2^3}} = \frac{2^9}{3^8} = \frac{512}{6561}$. $a_4 = \frac{2^{4^2}}{4^{2^4}} = \frac{2^{16}}{4^{16}} = \frac{2^{16}}{(2^2)^{16}} = \frac{2^{16}}{2^{32}} = \frac{1}{2^{16}}$.

The structure of the terms does not lend itself to simplification using standard techniques for finding the sum of infinite series (e.g., geometric series, telescoping series, Taylor series). The complexity suggests that the sum cannot be easily calculated using elementary methods typically covered in JEE/NEET syllabi.

Given that the terms are strictly positive, their sum must also be positive. Therefore, the sum cannot be 0. If this question appeared in an exam where a simple numerical answer is expected, it might be flawed or intended as a trick question. In such a scenario, if 0 were an option, it would be based on a misunderstanding or misstatement of the problem, as the sum of positive terms cannot be zero.

Subject: Mathematics Chapter: Sequences and Series Topic: Infinite Series Difficulty: Hard Question Type: unknown