Question

In $\triangle ABC$, if $sin^2 A + sin^2 B = sin^2 C$ and $l(AB) = 10$, then the maximum value of the of triangle ABC is

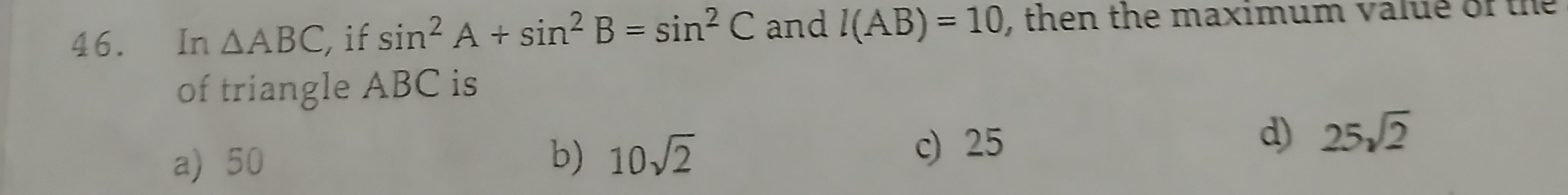
• A. 50
• B. $10\sqrt{2}$
• C. 25
• D. $25\sqrt{2}$

Answer 1

Answer: (C)

25

Answer 2

We are given that in a triangle ABC (with sides opposite angles A, B, C respectively) the following condition holds:

$$\sin^2 A + \sin^2 B = \sin^2 C$$

and that side $AB = 10$. In a triangle with vertices A, B, C, the side $AB$ is opposite angle C (i.e. $c=10$).

Step 1. Use the condition:

In any triangle, $A+B+C=\pi$ so that $C=\pi-(A+B)$. Thus,

$$\sin C = \sin\big[\pi-(A+B)\big] = \sin(A+B).$$

The given condition becomes:

$$\sin^2 A + \sin^2 B = \sin^2 (A+B).$$

Step 2. Expand $\sin^2(A+B)$:

Using the sine addition formula, we have:

$$\sin(A+B) = \sin A\cos B + \cos A\sin B.$$

Thus,

$$\sin^2 (A+B) = (\sin A\cos B+\cos A\sin B)^2 = \sin^2 A \cos^2 B + \cos^2 A \sin^2 B + 2\sin A\sin B\cos A\cos B.$$

So the equality becomes:

$$\sin^2 A + \sin^2 B = \sin^2 A \cos^2 B + \cos^2 A \sin^2 B + 2\sin A\sin B\cos A\cos B.$$

Step 3. Rearrange the equation:

Subtract the right-hand side terms from the left:

$$\sin^2 A + \sin^2 B - \sin^2 A\cos^2 B - \cos^2 A\sin^2 B = 2\sin A\sin B\cos A\cos B.$$

Notice that:

$$\sin^2 A (1-\cos^2 B) = \sin^2 A \sin^2 B \quad \text{and} \quad \sin^2 B (1-\cos^2 A) = \sin^2 A \sin^2 B.$$

Thus, the left-hand side becomes:

$$\sin^2 A\sin^2 B + \sin^2 A\sin^2 B = 2\sin^2 A \sin^2 B.$$

So,

$$2\sin^2 A\sin^2 B = 2\sin A\sin B\cos A\cos B.$$

Dividing both sides by $2\sin A\sin B$ (assuming none of the angles is 0, which is valid in a non-degenerate triangle) gives:

$$\sin A\sin B = \cos A\cos B.$$

Dividing by $\cos A\cos B$ (again nonzero):

$$\tan A \tan B = 1.$$

Step 4. Interpret the condition $\tan A\tan B=1$:

It is known that:

$$\cos(A+B) = \cos A\cos B - \sin A\sin B.$$

Thus, since $\sin A\sin B = \cos A\cos B$,

$$\cos(A+B) = \cos A\cos B - \cos A\cos B = 0.$$

So,

$$A+B = \frac{\pi}{2} \quad (\text{or } 90^\circ).$$

Then,

$$C = \pi - (A+B) = \frac{\pi}{2} = 90^\circ.$$

This shows that the triangle is right-angled at $C$.

Step 5. Maximizing the area of a right-angled triangle with fixed hypotenuse:

In a right triangle with hypotenuse $c=10$, if we denote the legs as $a$ and $b$, the area is

$$\text{Area} = \frac{1}{2}ab \quad \text{with} \quad a^2+b^2=10^2=100.$$

The product $ab$ is maximized when $a=b$. Then:

$$2a^2=100 \quad \Rightarrow \quad a^2=50 \quad \Rightarrow \quad a = 5\sqrt{2}.$$

Hence, the maximum area is:

$$\text{Area} = \frac{1}{2}(5\sqrt{2})(5\sqrt{2}) = \frac{1}{2}\times 50 = 25.$$

The maximum value (area) of triangle ABC is 25. Thus, the correct option is (c) 25.