Question

If

$\cos^5 x + \cos^5(x+\frac{2\pi}{3}) + \cos^5(x+\frac{4\pi}{3}) = 0$

then find the number of solution(s) in $[0,2\pi]$.

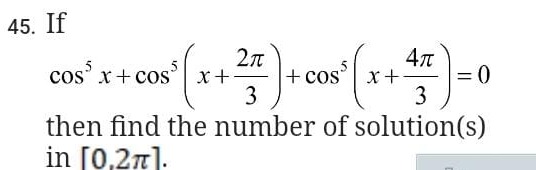
Answer 1

6 (There are 6 solutions in the interval $[0,2\pi]$).

Answer 2

Write $\cos^5\theta$ as $\frac{10\cos\theta+5\cos3\theta+\cos5\theta}{16}$.

Sum over the angles $x,\,x+\frac{2\pi}{3},\,x+\frac{4\pi}{3}$. The sums for $\cos\theta$ and $\cos5\theta$ vanish.

Only the $\cos3x$ term survives giving $\frac{15\cos3x}{16}=0$ so that $\cos3x=0$.

Solve $\cos3x=0 \Rightarrow x=\frac{\pi}{6}+\frac{k\pi}{3}$ and count 6 solutions in $[0,2\pi]$.