Question
Question: For an infinite line of charge having charge density $\lambda$ lying along x-axis, the work required...
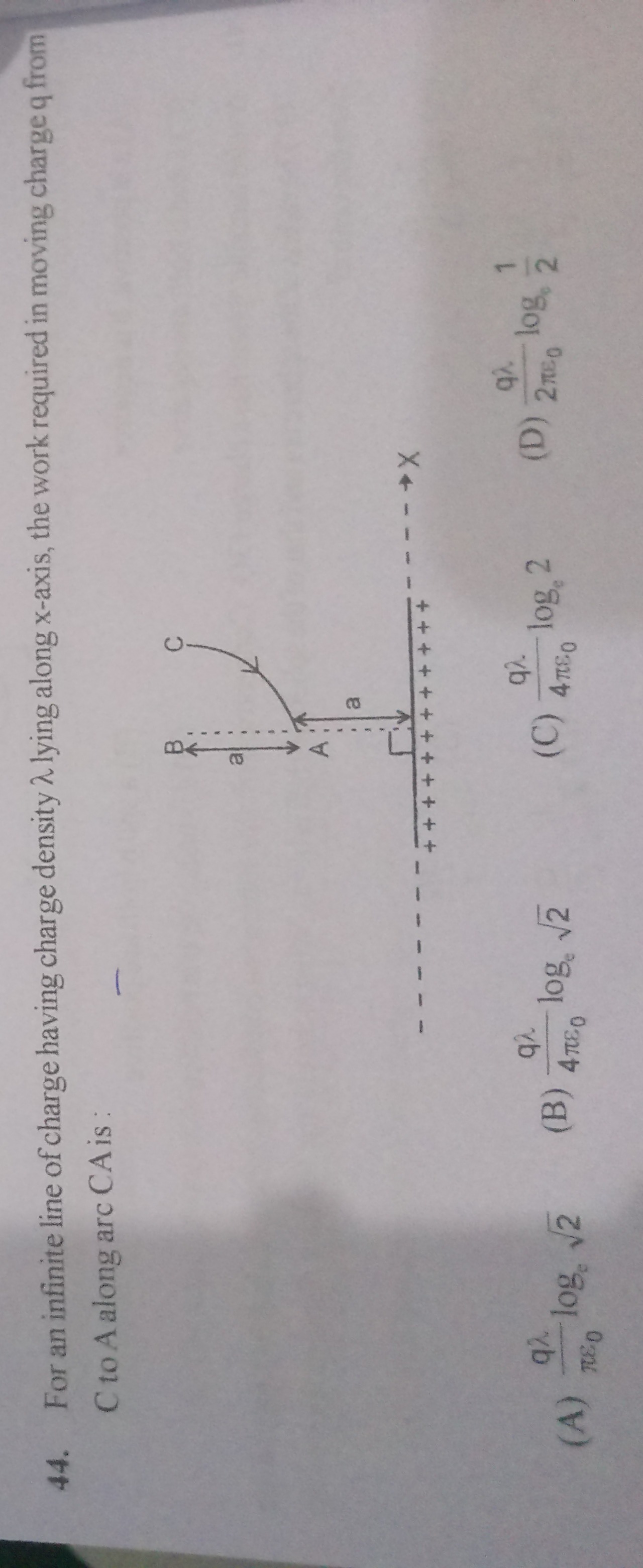
For an infinite line of charge having charge density λ lying along x-axis, the work required in moving charge q from C to A along arc CA is:
πϵ0qλloge2
4πϵ0qλloge2
4πϵ0qλloge2
2πϵ0qλloge21
4πϵ0qλloge2
Solution
The electric potential at a distance r from an infinite line of charge with linear charge density λ is given by:
V(r)=−2πϵ0λloger+K
where K is an arbitrary constant.
The work done in moving a charge q from point C to point A is:
WC→A=q(VA−VC)
The potential difference between points A and C is:
VA−VC=(−2πϵ0λlogerA+K)−(−2πϵ0λlogerC+K)=−2πϵ0λ(logerA−logerC)=2πϵ0λ(logerC−logerA)=2πϵ0λloge(rArC)
From the figure, assume that point C is located such that its distance from the x-axis is rC=2a, and point A is at a distance rA=a from the x-axis. This would make the ratio rC/rA=2.
Then the work done is:
WC→A=q(VA−VC)=q2πϵ0λloge(rArC)=q2πϵ0λloge(a2a)=q2πϵ0λloge2
Since loge2=2loge2, then loge2=21loge2.
Therefore, WC→A=2πϵ0qλloge2=2πϵ0qλ21loge2=4πϵ0qλloge2
