Question

Consider the function $f(x) = x\sqrt{1+(x+1)\sqrt{1+(x+2)\sqrt{1+(x+3)\sqrt{1+.....}}}}$, then $\lim_{n \to \infty} \sum_{x=1}^{n} \frac{1}{f(x)}$ is $\frac{p}{q}$ where p and q are coprime, then p + q is equal to

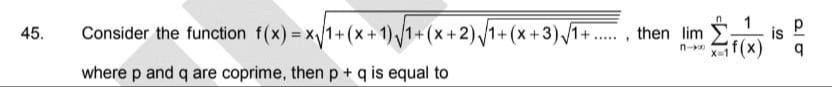
Answer 1

7

Answer 2

Solution:

We are given

$$f(x)=x\sqrt{1+(x+1)\sqrt{1+(x+2)\sqrt{1+(x+3)\sqrt{1+\cdots}}}}.$$

Define

$$g(x)=\sqrt{1+(x+1)\sqrt{1+(x+2)\sqrt{1+(x+3)\sqrt{1+\cdots}}}},$$

so that

$$f(x)=x\,g(x).$$

Notice that the “tail” of the nested radical has the same form (with a shift in $x$). In fact, we can write

$$g(x)=\sqrt{1+(x+1)\,g(x+1)}.$$

Now, we try a linear form for $g(x)$:

$$g(x)=a\,x+b.$$

Square both sides of the recurrence:

$$g(x)^2 =1+(x+1)\,g(x+1).$$

Substitute $g(x)=ax+b$ and $g(x+1)=a(x+1)+b=a\,x+(a+b)$. Then

$$(a\,x+b)^2 = 1+(x+1)[a\,x+(a+b)].$$

Expanding both sides:

$$a^2x^2+2ab\,x+b^2 = 1+a\,x^2+(2a+b)x+(a+b).$$

Equate coefficients for all powers of $x$:

1. Coefficient of $x^2$: $a^2=a$ ⟹ $a=1$ (since $a\ne0$).
2. Coefficient of $x$: $2b=2a+b$ ⟹ $2b=2+b$ ⟹ $b=2$.
3. Constant term: $b^2=1+(a+b)$ ⟹ $4=1+1+2=4$ (satisfied).

Thus,

$$g(x)=x+2\quad\text{and}\quad f(x)=x(x+2)=x^2+2x.$$

Now, consider the sum

$$S_n=\sum_{x=1}^{n}\frac{1}{f(x)}=\sum_{x=1}^{n}\frac{1}{x(x+2)}.$$

Decompose into partial fractions:

$$\frac{1}{x(x+2)}=\frac{1}{2}\left(\frac{1}{x}-\frac{1}{x+2}\right).$$

Thus,

$$S_n=\frac{1}{2}\sum_{x=1}^{n}\left(\frac{1}{x}-\frac{1}{x+2}\right).$$

Writing out terms we see telescoping:

$$S_n=\frac{1}{2}\Biggl[\left(\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\right)-\left(\frac{1}{3}+\frac{1}{4}+\cdots+\frac{1}{n+2}\right)\Biggr].$$

Everything cancels except:

$$S_n=\frac{1}{2}\left(\frac{1}{1}+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}\right).$$

Taking the limit as $n\to\infty$, the last two terms vanish:

$$\lim_{n\to\infty} S_n=\frac{1}{2}\left(1+\frac{1}{2}\right)=\frac{1}{2}\cdot\frac{3}{2}=\frac{3}{4}.$$

Here $\frac{3}{4}$ is in lowest terms, so $p=3$ and $q=4$.

Thus, $p+q=3+4=7$.

---

Minimal Explanation:

1. Write $f(x)=x\,g(x)$ where $g(x)=\sqrt{1+(x+1)g(x+1)}$.
2. Assume $g(x)=x+2$. Verification shows it works.
3. Hence, $f(x)=x(x+2)$ and $\displaystyle \frac{1}{f(x)}=\frac{1}{x(x+2)}=\frac{1}{2}\left(\frac{1}{x}-\frac{1}{x+2}\right)$.
4. Telescoping the series $\sum_{x=1}^n \frac{1}{f(x)}$ gives $\frac{1}{2}\left(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}\right)$, so the limit is $\frac{3}{4}$.
5. Therefore, $p+q=3+4=7$.