Question

A stationary $He^+$ ion emitted a photon corresponding to a first line of the Lyman series. The photon liberated a photoelectron from a stationary hydrogen atom in ground state. What is the speed (in $10^8$ cm/sec.) of photoelectron. (Ionisation energy of hydrogen atom = 13.6eV, e = 1.6 x $10^{-19}$ C. Mass of electron = 9.1 x $10^{-31}$ kg)

Answer 1

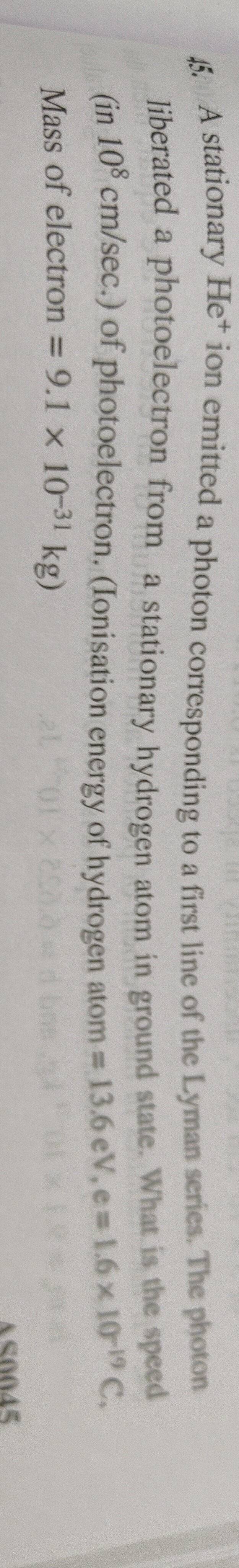
3.093

Answer 2

1. Photon energy from $He^+$ (Z=2) for the first Lyman line ($n=2 \to n=1$): $E_{photon} = 13.6 \times Z^2 \times (\frac{1}{1^2} - \frac{1}{2^2}) = 13.6 \times 2^2 \times \frac{3}{4} = 13.6 \times 3 = 40.8$ eV.

2. Work function for hydrogen ground state: $\phi = 13.6$ eV.

3. Kinetic energy of photoelectron: $KE = E_{photon} - \phi = 40.8 \text{ eV} - 13.6 \text{ eV} = 27.2$ eV.

4. Convert KE to Joules: $KE = 27.2 \times 1.6 \times 10^{-19} \text{ J} = 43.52 \times 10^{-19}$ J.

5. Calculate speed using $KE = \frac{1}{2}mv^2$: $v = \sqrt{\frac{2 \times KE}{m}} = \sqrt{\frac{2 \times 43.52 \times 10^{-19}}{9.1 \times 10^{-31}}} \approx 3.0927 \times 10^6$ m/s.

6. Convert to cm/sec: $v \approx 3.0927 \times 10^6 \times 100 \text{ cm/s} = 3.0927 \times 10^8$ cm/s.

The speed is approximately $3.093 \times 10^8$ cm/sec. The value in $10^8$ cm/sec is 3.093.