Solveeit Logo
Login

Question

Question: Let $f(x) = \int_{0}^{x} (t + \sin(1-e^t)) dt, x \in R$. Then, $\lim_{x \to 0} \frac{f(x)}{x^3}$ is ...

Let f(x)=∫0x(t+sin⁡(1−et))dt,x∈Rf(x) = \int_{0}^{x} (t + \sin(1-e^t)) dt, x \in R. Then, lim⁡x→0f(x)x3\lim_{x \to 0} \frac{f(x)}{x^3} is equal to:

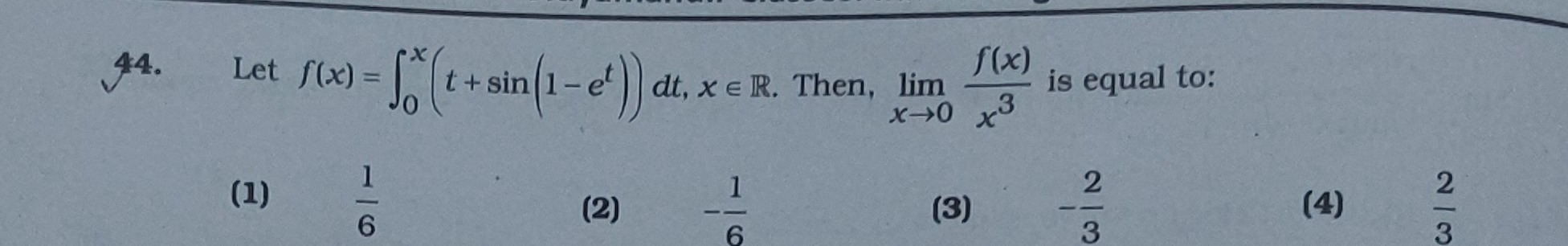
A

1/6

B

-1/6

C

-2/3

D

2/3

Answer

-1/6

Explanation

Solution

Since f(0)=0f(0) = 0, the limit is of the indeterminate form 00\frac{0}{0}. We apply L'Hôpital's Rule three times.

  1. First application: lim⁡x→0f(x)x3=lim⁡x→0f′(x)3x2=lim⁡x→0x+sin⁡(1−ex)3x2\lim_{x \to 0} \frac{f(x)}{x^3} = \lim_{x \to 0} \frac{f'(x)}{3x^2} = \lim_{x \to 0} \frac{x + \sin(1-e^x)}{3x^2} (still 00\frac{0}{0}).

  2. Second application: lim⁡x→01−excos⁡(1−ex)6x\lim_{x \to 0} \frac{1 - e^x \cos(1-e^x)}{6x} (still 00\frac{0}{0}).

  3. Third application: lim⁡x→0−[excos⁡(1−ex)+e2xsin⁡(1−ex)]6\lim_{x \to 0} \frac{-[e^x \cos(1-e^x) + e^{2x} \sin(1-e^x)]}{6}

Evaluating at x=0x=0: −[e0cos⁡(1−e0)+e0sin⁡(1−e0)]6=−[1⋅cos⁡(0)+1⋅sin⁡(0)]6=−[1⋅1+1⋅0]6=−16\frac{-[e^0 \cos(1-e^0) + e^{0} \sin(1-e^0)]}{6} = \frac{-[1 \cdot \cos(0) + 1 \cdot \sin(0)]}{6} = \frac{-[1 \cdot 1 + 1 \cdot 0]}{6} = -\frac{1}{6}.