Solveeit Logo
Login

Question

Question: 43. The value of $\tan^{-1}(1) \cos^{-1}(-\frac{1}{2}) + \sin^{-1}(-\frac{1}{2})$...

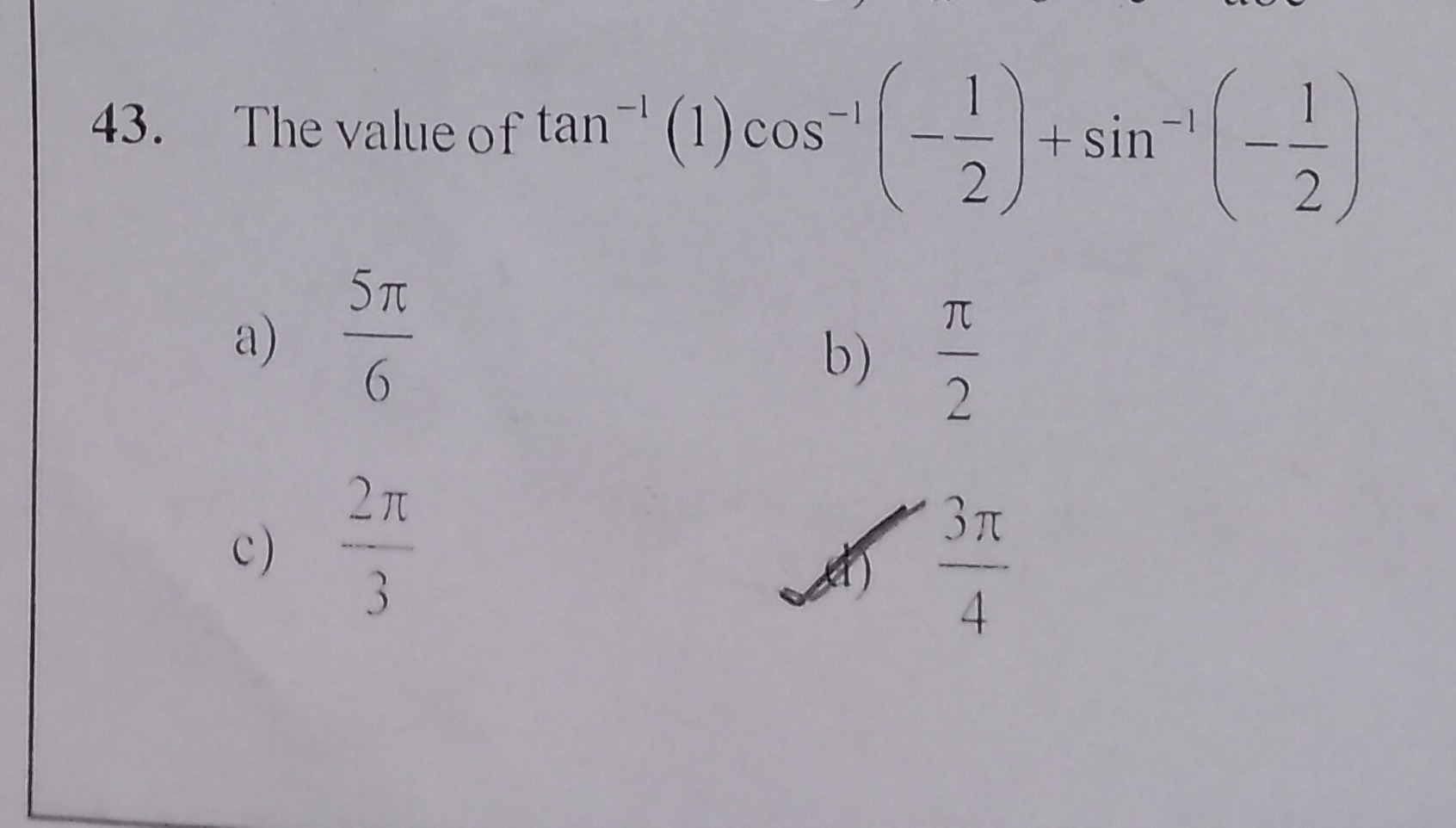
  1. The value of tan⁡−1(1)cos⁡−1(−12)+sin⁡−1(−12)\tan^{-1}(1) \cos^{-1}(-\frac{1}{2}) + \sin^{-1}(-\frac{1}{2})
A

5π6\frac{5\pi}{6}

B

π2\frac{\pi}{2}

C

2π3\frac{2\pi}{3}

D

3π4\frac{3\pi}{4}

Answer

3π4\displaystyle \frac{3\pi}{4}

Explanation

Solution

Solution Explanation:
It is most likely that the intended expression is

tan⁡−1(1)+cos⁡−1(−12)+sin⁡−1(−12).\tan^{-1}(1) + \cos^{-1}\Bigl(-\frac{1}{2}\Bigr) + \sin^{-1}\Bigl(-\frac{1}{2}\Bigr).

Now,

tan⁡−1(1)=π4,cos⁡−1(−12)=2π3,sin⁡−1(−12)=−π6.\tan^{-1}(1)=\frac{\pi}{4}, \quad \cos^{-1}\Bigl(-\frac{1}{2}\Bigr)=\frac{2\pi}{3}, \quad \sin^{-1}\Bigl(-\frac{1}{2}\Bigr)=-\frac{\pi}{6}.

Adding these gives:

π4+2π3−π6=(3π12+8π12−2π12)=9π12=3π4.\frac{\pi}{4}+\frac{2\pi}{3}-\frac{\pi}{6}=\left(\frac{3\pi}{12}+\frac{8\pi}{12}-\frac{2\pi}{12}\right)=\frac{9\pi}{12}=\frac{3\pi}{4}.

Answer:
3π4\displaystyle \frac{3\pi}{4} (Option d)