Question

The ratio of wavelength of deutron and proto accelerated through the same potential difference will be -

• A. $\frac{1}{\sqrt{2}}$
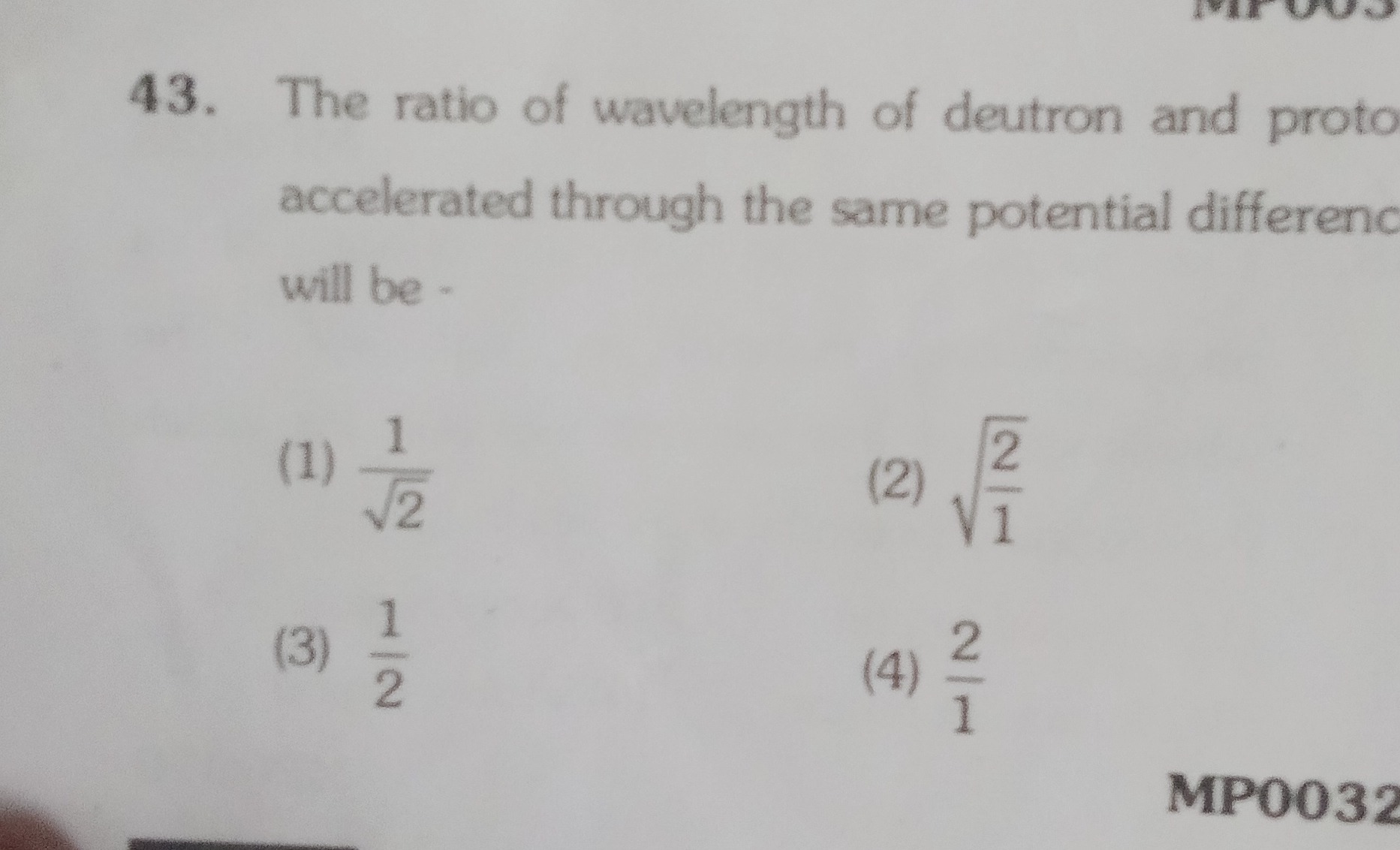
• B. $\sqrt{\frac{2}{1}}$
• C. $\frac{1}{2}$
• D. $\frac{2}{1}$

Answer 1

Answer: (A)

(1) $\frac{1}{\sqrt{2}}$

Answer 2

The de-Broglie wavelength ($\lambda$) for a charged particle of mass $m$ and charge $q$ accelerated through a potential difference $V$ is given by the formula:

$\lambda = \frac{h}{p}$

where $h$ is Planck's constant and $p$ is the momentum of the particle. The kinetic energy ($K$) gained by the particle is $K = qV$. Also, kinetic energy is related to momentum by $K = \frac{p^2}{2m}$. Equating the two expressions for kinetic energy, we get:

$qV = \frac{p^2}{2m}$

$p^2 = 2mqV$

$p = \sqrt{2mqV}$

Substituting this into the de-Broglie wavelength formula:

$\lambda = \frac{h}{\sqrt{2mqV}}$

Now, let's apply this formula to a proton (p) and a deuteron (d).

For a proton: Mass of proton ($m_p$) = $m$ (let's denote it as $m$) Charge of proton ($q_p$) = $e$ (let's denote it as $e$) Potential difference ($V_p$) = $V$ (given as same for both) The de-Broglie wavelength of the proton ($\lambda_p$) is:

$\lambda_p = \frac{h}{\sqrt{2m_p e V}}$

For a deuteron: A deuteron is the nucleus of deuterium, consisting of one proton and one neutron. Mass of deuteron ($m_d$) $\approx$ mass of proton + mass of neutron. Since the mass of a neutron is approximately equal to the mass of a proton, $m_d \approx m_p + m_p = 2m_p$. Charge of deuteron ($q_d$) = charge of one proton = $e$. Potential difference ($V_d$) = $V$ (given as same for both) The de-Broglie wavelength of the deuteron ($\lambda_d$) is:

$\lambda_d = \frac{h}{\sqrt{2m_d e V}}$

We need to find the ratio of the wavelength of the deuteron to the proton, i.e., $\frac{\lambda_d}{\lambda_p}$.

$\frac{\lambda_d}{\lambda_p} = \frac{\frac{h}{\sqrt{2m_d e V}}}{\frac{h}{\sqrt{2m_p e V}}}$

$\frac{\lambda_d}{\lambda_p} = \frac{\sqrt{2m_p e V}}{\sqrt{2m_d e V}}$

$\frac{\lambda_d}{\lambda_p} = \sqrt{\frac{2m_p e V}{2m_d e V}}$

$\frac{\lambda_d}{\lambda_p} = \sqrt{\frac{m_p}{m_d}}$

Substitute $m_d = 2m_p$:

$\frac{\lambda_d}{\lambda_p} = \sqrt{\frac{m_p}{2m_p}}$

$\frac{\lambda_d}{\lambda_p} = \sqrt{\frac{1}{2}}$

$\frac{\lambda_d}{\lambda_p} = \frac{1}{\sqrt{2}}$