Question

If shortest wavelength of H-atom in Balmer series is xÅ then, (i) The shortest wave length in Lyman series is $\frac{x}{y}$Å. The value of 'y' is. (ii) The longest wave length in Paschen series is $\frac{x}{z}$Å. The value of 'z' is.

Answer 1

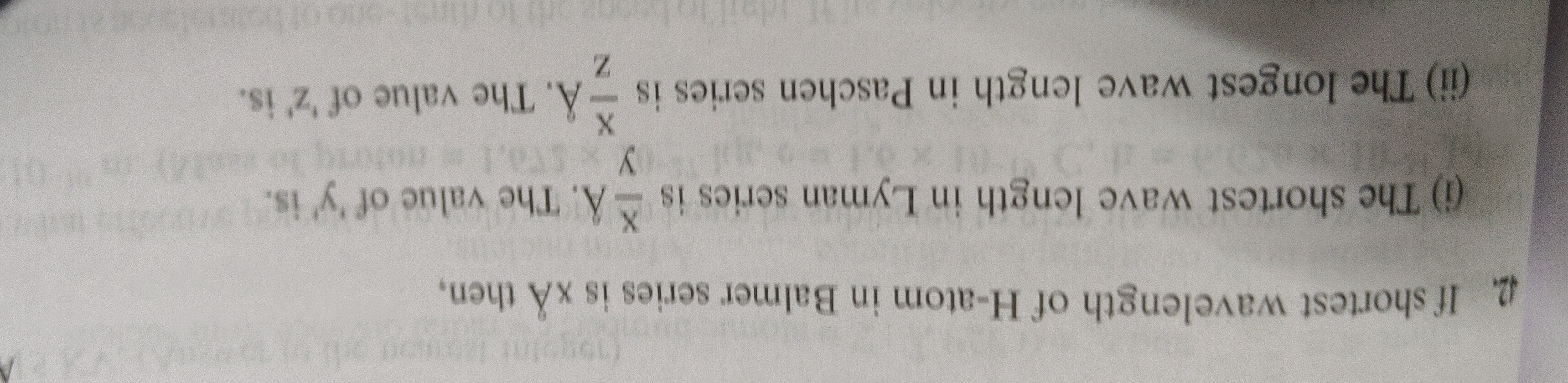
For (i): y = 4. For (ii): z = 7/36.

Answer 2

The Rydberg formula for the wavelength of spectral lines is: $\frac{1}{\lambda} = RZ^2 \left( \frac{1}{n_f^2} - \frac{1}{n_i^2} \right)$ For a Hydrogen atom, $Z=1$.

The shortest wavelength in the Balmer series corresponds to the transition from $n_i = \infty$ to $n_f = 2$. Given this shortest wavelength is $x$ Å: $\frac{1}{x} = R \left( \frac{1}{2^2} - \frac{1}{\infty^2} \right) = R \left( \frac{1}{4} \right)$ This implies $R = \frac{4}{x}$.

(i) The shortest wavelength in the Lyman series corresponds to the transition from $n_i = \infty$ to $n_f = 1$. $\frac{1}{\lambda_L} = R \left( \frac{1}{1^2} - \frac{1}{\infty^2} \right) = R$ Substituting the value of $R$: $\frac{1}{\lambda_L} = \frac{4}{x} \implies \lambda_L = \frac{x}{4}$ Given $\lambda_L = \frac{x}{y}$, we find $y = 4$.

(ii) The longest wavelength in the Paschen series corresponds to the transition from $n_i = 4$ to $n_f = 3$ (the smallest energy difference for $n_f=3$). $\frac{1}{\lambda_P} = R \left( \frac{1}{3^2} - \frac{1}{4^2} \right) = R \left( \frac{1}{9} - \frac{1}{16} \right) = R \left( \frac{16 - 9}{144} \right) = R \left( \frac{7}{144} \right)$ Substituting the value of $R$: $\frac{1}{\lambda_P} = \frac{4}{x} \left( \frac{7}{144} \right) = \frac{28}{144x} = \frac{7}{36x}$ Therefore, $\lambda_P = \frac{36x}{7}$. Given $\lambda_P = \frac{x}{z}$, we have: $\frac{36x}{7} = \frac{x}{z} \implies z = \frac{7}{36}$