Question

Let the curve $y = y(x)$ be the solution of the differential equation, $\frac{dy}{dx} = 2(x+1)$. If the numerical value of area bounded by the curve $y = y(x)$ and x-axis is $\frac{4\sqrt{8}}{3}$, then the value of y(1) is equal to ____.

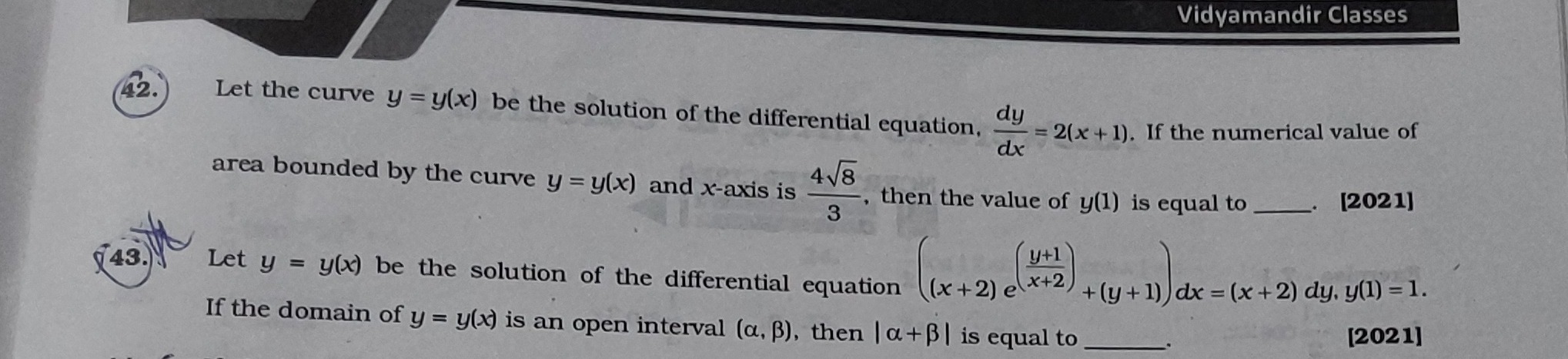
Answer 1

2

Answer 2

1. Integrate $\frac{dy}{dx} = 2(x+1)$ to get $y = x^2 + 2x + C$.

2. Identify roots of $y=0$ as $x = -1 \pm \sqrt{1-C}$.

3. Use the area formula for a parabola $A = \frac{|a|}{6}(x_2-x_1)^3$. Substitute $a=1$ and $x_2-x_1=2\sqrt{1-C}$ to get $A = \frac{4}{3}(1-C)^{3/2}$.

4. Equate this to the given area $\frac{4\sqrt{8}}{3} = \frac{8\sqrt{2}}{3}$.

5. Solve for $C$: $(1-C)^{3/2} = 2\sqrt{2} = 2^{3/2} \implies 1-C=2 \implies C=-1$.

6. Substitute $C=-1$ into $y=x^2+2x+C$ to get $y=x^2+2x-1$.

7. Calculate $y(1) = 1^2+2(1)-1 = 2$.