Question

Let $\bar{u}$ be a vector coplanar with the vectors $\bar{a} = 2\hat{i} +3\hat{j}-\hat{k}$ and $\bar{b} = \hat{j} + \hat{k}$. If $\bar{u}$ is perpendicular

to $\bar{a}$ and $\bar{u}.\bar{b} = 24$, then $|\bar{u}|^2 =$

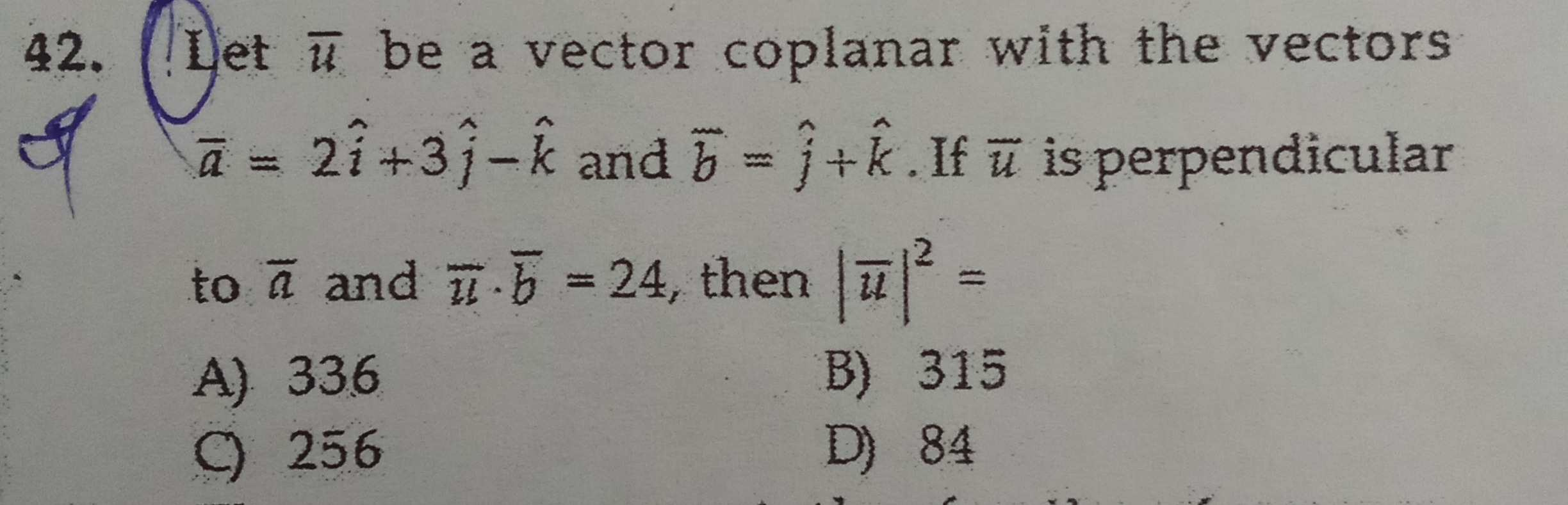
• A. 336
• B. 315
• C. 256
• D. 84

Answer 1

Answer: (A)

336

Answer 2

To solve this problem:

1. Express $\vec{u}$ as a linear combination of $\vec{a}$ and $\vec{b}$:
   $\vec{u} = m\vec{a} + n\vec{b}$.

2. Use the perpendicularity condition $\vec{u} \cdot \vec{a} = 0$ to find a relationship between $m$ and $n$.

   • Compute $\vec{a} \cdot \vec{a} = 2^2 + 3^2 + (-1)^2 = 14$ and $\vec{a} \cdot \vec{b} = (2)(0) + (3)(1) + (-1)(1) = 2$.
   • This gives $14m + 2n = 0$, which simplifies to $n = -7m$.

3. Use the condition $\vec{u} \cdot \vec{b} = 24$ to solve for $m$ and $n$.

   • We have $\vec{u} \cdot \vec{b} = m(\vec{a} \cdot \vec{b}) + n(\vec{b} \cdot \vec{b}) = 2m + 2n = 24$.
   • Substituting $n = -7m$, we get $2m + 2(-7m) = 2m - 14m = -12m = 24$, so $m = -2$.
   • Then, $n = -7(-2) = 14$.

4. Compute $\vec{u} = -2\vec{a} + 14\vec{b}$.

5. Calculate $|\vec{u}|^2$:

   • $|\vec{u}|^2 = (-2\vec{a} + 14\vec{b}) \cdot (-2\vec{a} + 14\vec{b}) = 4|\vec{a}|^2 + 196|\vec{b}|^2 - 56(\vec{a} \cdot \vec{b})$.
   • Substitute the computed values: $|\vec{a}|^2 = 14$, $|\vec{b}|^2 = 2$, $\vec{a} \cdot \vec{b} = 2$.
   • $|\vec{u}|^2 = 4(14) + 196(2) - 56(2) = 56 + 392 - 112 = 336$.

Therefore, $|\vec{u}|^2 = 336$.