Question

Let $A = \begin{bmatrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1 \end{bmatrix}$ and $10B = \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix}$. If B is the inverse of A. Then $\alpha$ is equal to

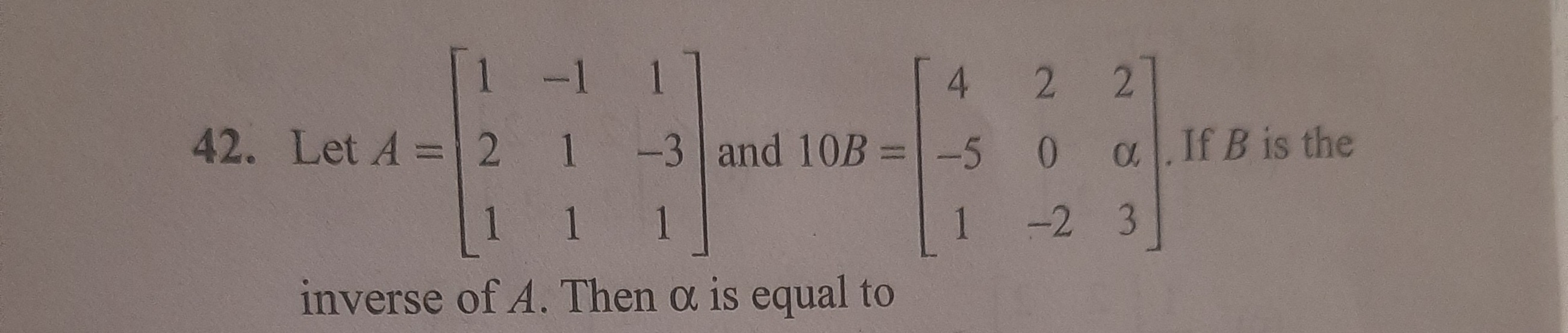
Answer 1

$\alpha = 5$

Answer 2

1. Find det A:

   $$\det(A) = 1\det\begin{bmatrix} 1 & -3 \\ 1 & 1 \end{bmatrix} - (-1)\det\begin{bmatrix} 2 & -3 \\ 1 & 1 \end{bmatrix} + 1\det\begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix}$$ $$= 1(1\cdot1- (-3)\cdot1) + 1(2\cdot1-(-3)\cdot1) + 1(2\cdot1-1\cdot1)$$ $$= 1(4) + 1(5) + 1(1) = 10.$$

2. Find the adjugate of A:

   • $C_{11} = +\det\begin{bmatrix} 1 & -3 \\ 1 & 1 \end{bmatrix} = 4$

   • $C_{12} = -\det\begin{bmatrix} 2 & -3 \\ 1 & 1 \end{bmatrix} = -5$

   • $C_{13} = +\det\begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} = 1$

   • $C_{21} = -\det\begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix} = 2$

   • $C_{22} = +\det\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} = 0$

   • $C_{23} = -\det\begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix} = -2$

   • $C_{31} = +\det\begin{bmatrix} -1 & 1 \\ 1 & -3 \end{bmatrix} = 2$

   • $C_{32} = -\det\begin{bmatrix} 1 & 1 \\ 2 & -3 \end{bmatrix} = 5$

   • $C_{33} = +\det\begin{bmatrix} 1 & -1 \\ 2 & 1 \end{bmatrix} = 3$

   The cofactor matrix is:

   $$\begin{bmatrix} 4 & -5 & 1 \\ 2 & 0 & -2 \\ 2 & 5 & 3 \end{bmatrix}$$

   Taking its transpose (to get the adjugate):

   $$\text{adj}(A) = \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & 5 \\ 1 & -2 & 3 \end{bmatrix}$$

3. Compute $A^{-1}$:

   $$A^{-1} = \frac{1}{\det A}\text{adj}(A) = \frac{1}{10} \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & 5 \\ 1 & -2 & 3 \end{bmatrix}$$

4. Given that $B$ is $A^{-1}$ and $10B$ is:

   $$10B = \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix}$$

   Equate the (2,3) entry: In $10A^{-1}$ the (2,3) entry is $5$, hence:

   $$\alpha = 5.$$