Question

Let $A = \begin{bmatrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1 \end{bmatrix}$ and $10B = \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix}$. If $B$ is the inverse of $A$. Then $\alpha$ is equal to

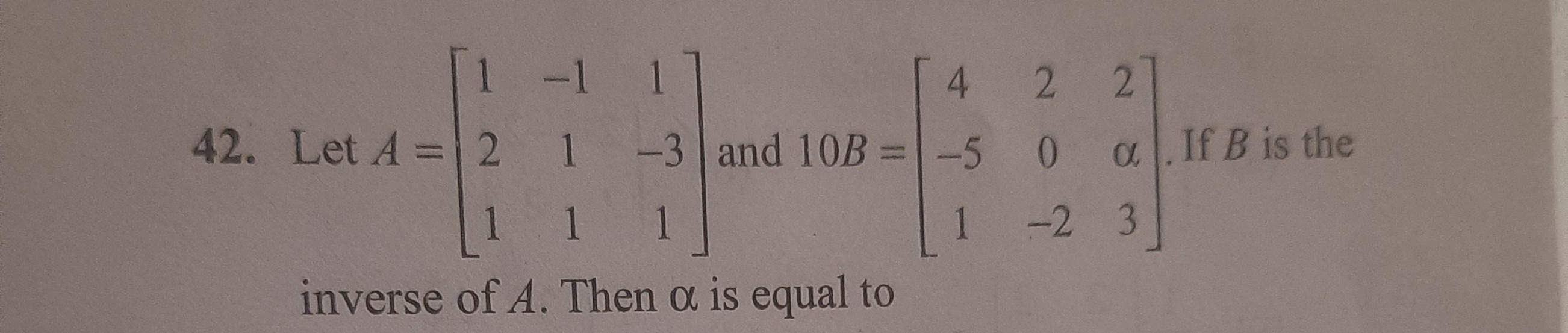
Answer 1

5

Answer 2

Given

$$A = \begin{bmatrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1 \end{bmatrix} \quad \text{and} \quad 10B = \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix},$$

with $B = A^{-1}$. Thus,

$$A^{-1} = \frac{1}{10}\begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix}.$$

Since $AA^{-1} = I$, we have:

$$A \left(\frac{1}{10}\begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix}\right) = I \quad \Longrightarrow \quad A \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix} = 10\,I.$$

Step 1: Compute the first row of $AX$ (where $X$ denotes the given $10B$ matrix):

• Row 1 of $A$ is $[1, -1, 1]$.

For the third column:

$$(1)(2) + (-1)(\alpha) + (1)(3) = 2 - \alpha + 3 = 5 - \alpha.$$

Since this entry must equal 0 (as it is an off-diagonal element of $10I$), we get:

$$5 - \alpha = 0 \quad \Longrightarrow \quad \alpha = 5.$$