Question

Let $A = \begin{bmatrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1 \end{bmatrix}$ and $10B = \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix}$. If $B$ is the inverse of $A$. Then $\alpha$ is equal to

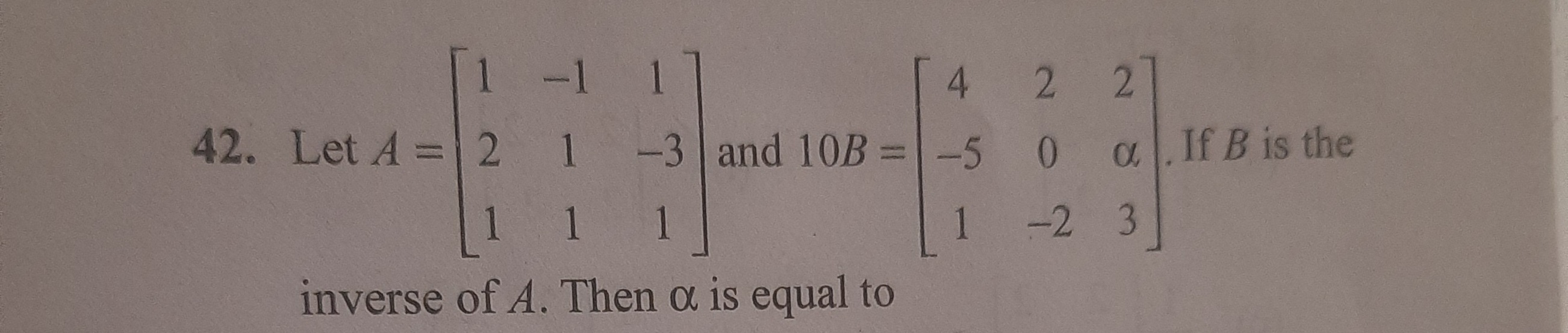
Answer 1

5

Answer 2

Given

$$A = \begin{bmatrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1 \end{bmatrix} \quad \text{and} \quad 10B = \begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix}.$$

Since $B$ is the inverse of $A$, we have $A \cdot B = I$. Note that

$$B = \frac{1}{10}\begin{bmatrix} 4 & 2 & 2 \\ -5 & 0 & \alpha \\ 1 & -2 & 3 \end{bmatrix}.$$

Step 1: Compute the $(1,3)$ entry of $A \cdot B$.

• First row of $A$: $[1, -1, 1]$
• Third column of $B$: $\frac{1}{10}\begin{bmatrix} 2 \\ \alpha \\ 3 \end{bmatrix}$

Thus,

$$(1,3) \text{ entry} = \frac{1}{10} \left(1\cdot2 + (-1)\cdot\alpha + 1\cdot3\right) = \frac{1}{10}(2 - \alpha + 3) = \frac{1}{10}(5 - \alpha).$$

For $A \cdot B = I$, the $(1,3)$ entry must be 0. Therefore,

$$\frac{5-\alpha}{10} = 0 \quad \Rightarrow \quad 5 - \alpha = 0 \quad \Rightarrow \quad \alpha = 5.$$

Core Explanation:

• Set up $A\cdot B=I$.
• Compute $(1,3)$ element: $\frac{5-\alpha}{10}=0$.
• Solve for $\alpha$: $\alpha=5$.

Answer: $\alpha = 5$.