Question
Question: 42. In a $\triangle ABC$, if $a=10$, $\tan A = \frac{3}{4}$, then $R=$...
- In a △ABC, if a=10, tanA=43, then R=
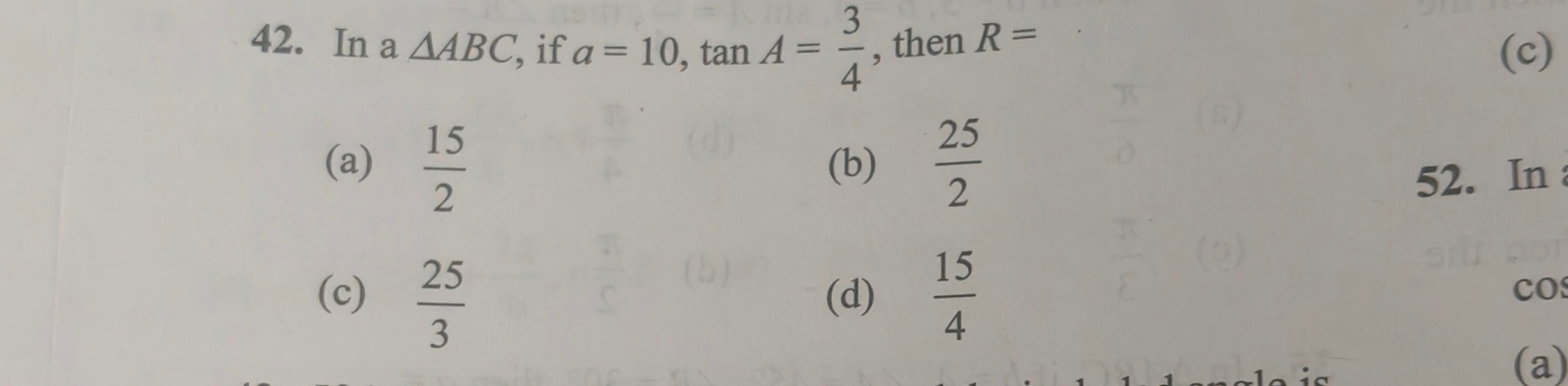
A
215
B
225
C
325
D
415
Answer
325
Explanation
Solution
Given: In ΔABC, side a=10 and tanA=43.
- From tanA=43, construct a right triangle with opposite = 3 and adjacent = 4, so the hypotenuse = 5.
- Thus, sinA=53.
- Using the extended sine law: a=2RsinA⇒R=2sinAa=2×5310=5610=610×5=650=325
