Question

If $y = \sqrt{\frac{1-\sin^{-1}x}{1+\sin^{-1}x}}$, then $\left(\frac{dy}{dx}\right)$ at $x = 0$ is

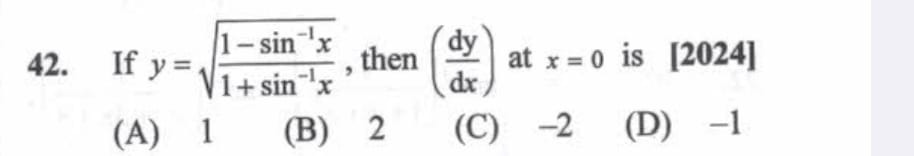
• A. 1
• B. 2
• C. -2
• D. -1

Answer 1

Answer: (D)

-1

Answer 2

Let $u=\sin^{-1}x$. Then $y = \sqrt{\frac{1-u}{1+u}}$.
Using logarithmic differentiation:

1. Take logarithm:

   $$\ln y = \frac{1}{2} \left[\ln(1-u) - \ln(1+u)\right]$$

2. Differentiate with respect to $u$:

   $$\frac{1}{y}\frac{dy}{du} = \frac{1}{2}\left[-\frac{1}{1-u} - \frac{1}{1+u}\right]$$ $$\frac{dy}{du} = y \left[-\frac{1}{2} \left(\frac{1}{1-u} + \frac{1}{1+u}\right)\right]$$

3. At $x = 0$, we have $u = \sin^{-1}(0) = 0$ and

   $$y = \sqrt{\frac{1-0}{1+0}} = 1.$$

   So,

   $$\left.\frac{dy}{du}\right|_{u=0} = -\frac{1}{2}\left(\frac{1}{1} + \frac{1}{1}\right) = -\frac{1}{2}(2) = -1.$$

4. Now, differentiate $u = \sin^{-1}x$ with respect to $x$:

   $$\frac{du}{dx} = \frac{1}{\sqrt{1-x^2}},$$

   and at $x = 0$, $\frac{du}{dx} = 1$.

5. Therefore, by the chain rule:

   $$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} = -1 \times 1 = -1.$$