Question

42. If $\tan^{-1} a + \tan^{-1} b + \tan^{-1} c = \pi$, then which of the following statement is true ?

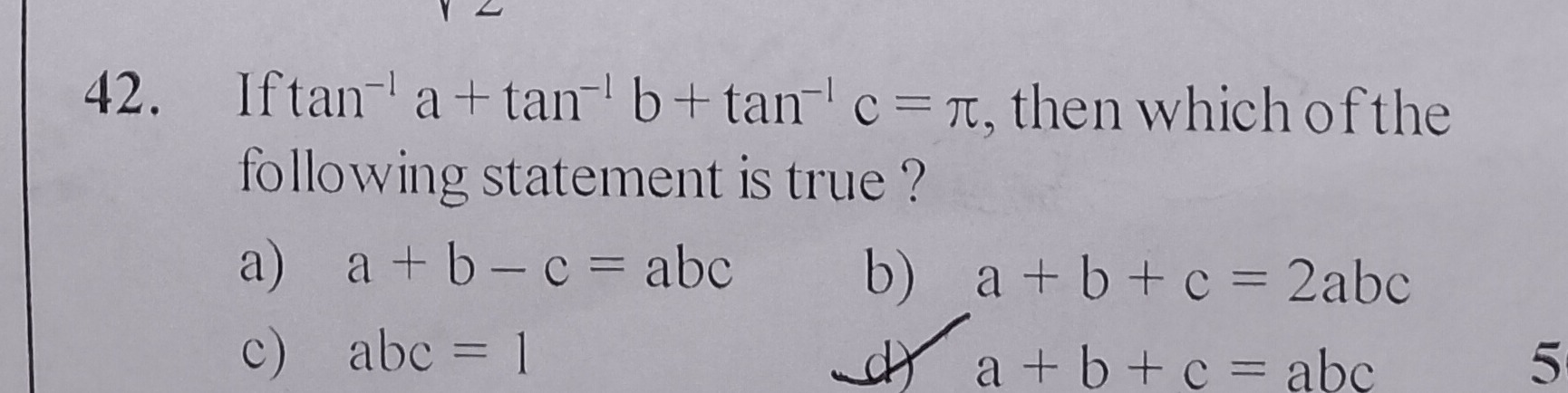
• A. a + b − c = abc
• B. a + b + c = 2abc
• C. abc = 1
• D. a + b + c = abc

Answer 1

Answer: (D)

a + b + c = abc

Answer 2

Let

$$X = \tan^{-1} a,\quad Y = \tan^{-1} b,\quad Z = \tan^{-1} c$$

Given,

$$X+Y+Z = \pi$$

Using the tangent addition formula for two angles:

$$\tan (X+Y) = \frac{a+b}{1-ab}$$

Then,

$$\tan (X+Y+Z) = \frac{\tan(X+Y) + c}{1 - c\,\tan(X+Y)} = 0$$

For the fraction to be 0, the numerator must be 0, so:

$$\frac{a+b}{1-ab} + c = 0 \quad \Longrightarrow \quad a+b + c(1-ab) = 0$$

Expanding,

$$a+b+c - abc = 0 \quad \Longrightarrow \quad a+b+c = abc$$