Question
Question: If $I_{1} = \int_{0}^{1} \frac{x^{5/2}(1-x)^{7/2}}{12} dx$; $I_{2} = \int_{0}^{1} \frac{x^{5/2}(1-x)...
If I1=∫0112x5/2(1−x)7/2dx; I2=∫01(3+x)8x5/2(1−x)7/2dx then
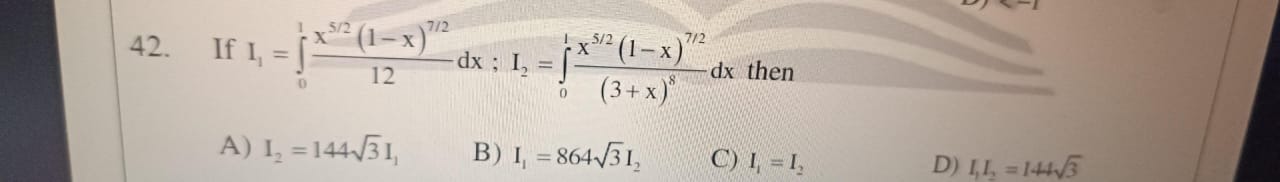
I2=1443I1
I1=8643I2
I1=I2
I1I2=1443
I1=8643I2
Solution
Let I1=∫0112x5/2(1−x)7/2dx and I2=∫01(3+x)8x5/2(1−x)7/2dx.
First, let's evaluate I1. The integral is related to the Beta function, B(m,n)=∫01xm−1(1−x)n−1dx=Γ(m+n)Γ(m)Γ(n). In the integral part of I1, we have x5/2(1−x)7/2. Comparing with xm−1(1−x)n−1, we have m−1=5/2⟹m=7/2 and n−1=7/2⟹n=9/2. So, ∫01x5/2(1−x)7/2dx=B(7/2,9/2). I1=121B(7/2,9/2)=121Γ(7/2+9/2)Γ(7/2)Γ(9/2)=121Γ(8)Γ(7/2)Γ(9/2). Using the property Γ(z+1)=zΓ(z) and Γ(1/2)=π: Γ(7/2)=25Γ(5/2)=25⋅23Γ(3/2)=25⋅23⋅21Γ(1/2)=815π. Γ(9/2)=27Γ(7/2)=27⋅815π=16105π. Γ(8)=7!=5040. B(7/2,9/2)=5040(815π)(16105π)=50408×1615×105π=128×50401575π. 50401575=720×7225×7=720225=144×545×5=14445=16×95×9=165. So, B(7/2,9/2)=1285π. I1=121⋅1285π=15365π.
Now, let's evaluate I2=∫01(3+x)8x5/2(1−x)7/2dx. This integral is of the form ∫01(c+dx)a+bxa−1(1−x)b−1dx. Here, a−1=5/2⟹a=7/2, b−1=7/2⟹b=9/2. a+b=7/2+9/2=16/2=8. The denominator is (3+x)8, which matches (c+dx)a+b with c=3 and d=1. We use the integral formula: ∫01(c+dx)a+bxa−1(1−x)b−1dx=(c+d)acb1B(a,b). In our case, a=7/2, b=9/2, c=3, d=1. I2=(3+1)7/239/21B(7/2,9/2)=47/239/21B(7/2,9/2). 47/2=(22)7/2=27=128. 39/2=343=813. I2=128⋅8131B(7/2,9/2). We know B(7/2,9/2)=1285π. I2=128⋅8131⋅1285π=1282⋅8135π=16384⋅8135π.
Now let's find the relationship between I1 and I2. I1=121B(7/2,9/2). I2=128⋅8131B(7/2,9/2). Let B=B(7/2,9/2). I1=121B. I2=128⋅8131B. Divide I1 by I2: I2I1=128⋅8131B121B=121⋅(128⋅813)=12128⋅813=4⋅3128⋅27⋅33=32⋅273=8643. So, I1=8643I2.
