Solveeit Logo
Login

Question

Question: Differential co-efficient of $e^{sin^{-1}x}$ w.r.t. $x sin^{-1}x$ is...

Differential co-efficient of esin−1xe^{sin^{-1}x} w.r.t. xsin−1xx sin^{-1}x is

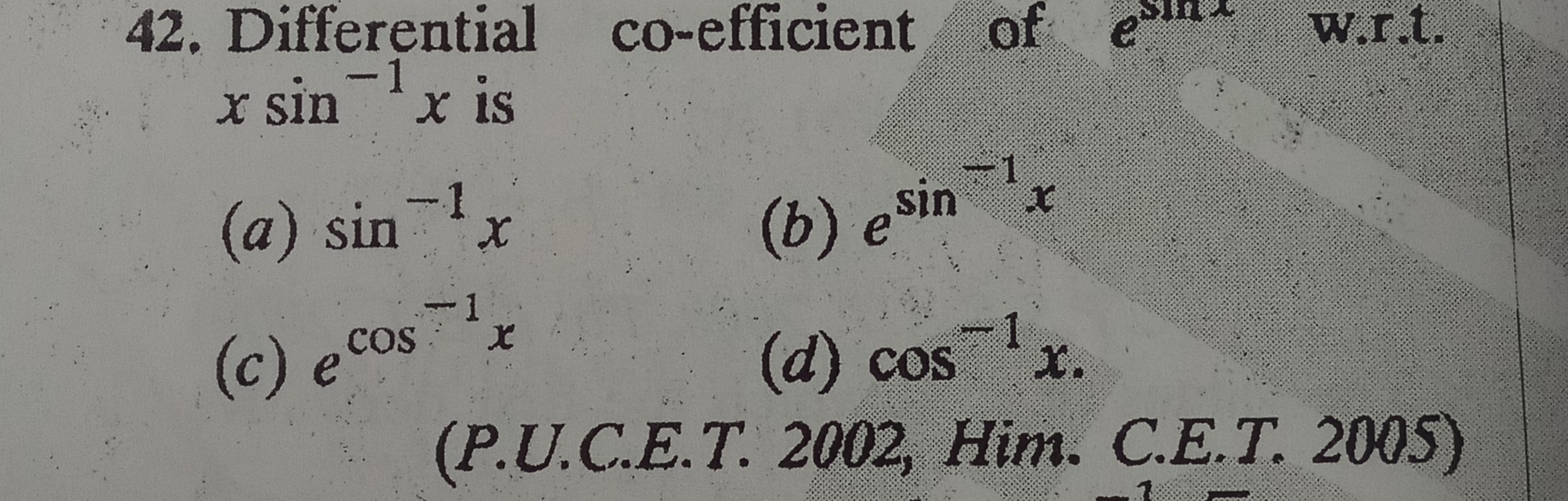
A

sin−1xsin^{-1}x

B

esin−1xe^{sin^{-1}x}

C

ecos−1xe^{cos^{-1}x}

D

cos−1xcos^{-1}x

Answer

esin⁡−1xx+1−x2 sin⁡−1x\frac{e^{\sin^{-1}x}}{x+\sqrt{1-x^2}\,\sin^{-1}x}

Explanation

Solution

We wish to find

dd [xsin⁡−1x](esin⁡−1x)=d(esin⁡−1x)/dxd(xsin⁡−1x)/dx.\frac{d}{d\,[x\sin^{-1}x]}\Bigl(e^{\sin^{-1}x}\Bigr) =\frac{d\Bigl(e^{\sin^{-1}x}\Bigr)/dx}{d\Bigl(x\sin^{-1}x\Bigr)/dx}.

Step 1. Write

f(x)=esin⁡−1x .f(x)=e^{\sin^{-1}x}\,.

Differentiate with respect to xx using the chain rule:

f′(x)=esin⁡−1x⋅ddx(sin⁡−1x)=esin⁡−1x⋅11−x2 .f'(x)= e^{\sin^{-1}x}\cdot \frac{d}{dx}(\sin^{-1}x) =e^{\sin^{-1}x}\cdot\frac{1}{\sqrt{1-x^2}}\,.

Step 2. Let

g(x)=xsin⁡−1x .g(x)=x\sin^{-1}x\,.

Differentiate using the product rule:

g′(x)=sin⁡−1x+x⋅11−x2=sin⁡−1x+x1−x2 .g'(x)= \sin^{-1}x+ x\cdot\frac{1}{\sqrt{1-x^2}} =\sin^{-1}x+\frac{x}{\sqrt{1-x^2}}\,.

Step 3. Hence the required derivative is

d (esin⁡−1x)d (xsin⁡−1x)=f′(x)g′(x)=esin⁡−1x/1−x2sin⁡−1x+x1−x2 .\frac{d\,(e^{\sin^{-1}x})}{d\,(x\sin^{-1}x)} =\frac{f'(x)}{g'(x)} =\frac{e^{\sin^{-1}x}/\sqrt{1-x^2}}{\sin^{-1}x+\dfrac{x}{\sqrt{1-x^2}}}\,.

Multiply numerator and denominator by 1−x2\sqrt{1-x^2} to write it in a slightly neater form:

d (esin⁡−1x)d (xsin⁡−1x)=esin⁡−1xx+1−x2 sin⁡−1x .\frac{d\,(e^{\sin^{-1}x})}{d\,(x\sin^{-1}x)} =\frac{e^{\sin^{-1}x}}{x+\sqrt{1-x^2}\,\sin^{-1}x}\,.

Final Answer:

esin⁡−1xx+1−x2 sin⁡−1x .\frac{e^{\sin^{-1}x}}{x+\sqrt{1-x^2}\,\sin^{-1}x}\,.

None of the given options is correct.