Question

A non uniform sphere can be kept on a rough inclined plane so that it is in equilibrium. In the fig below the dots represents location of centre of mass. In which one of the positions can sphere be equilibrium?

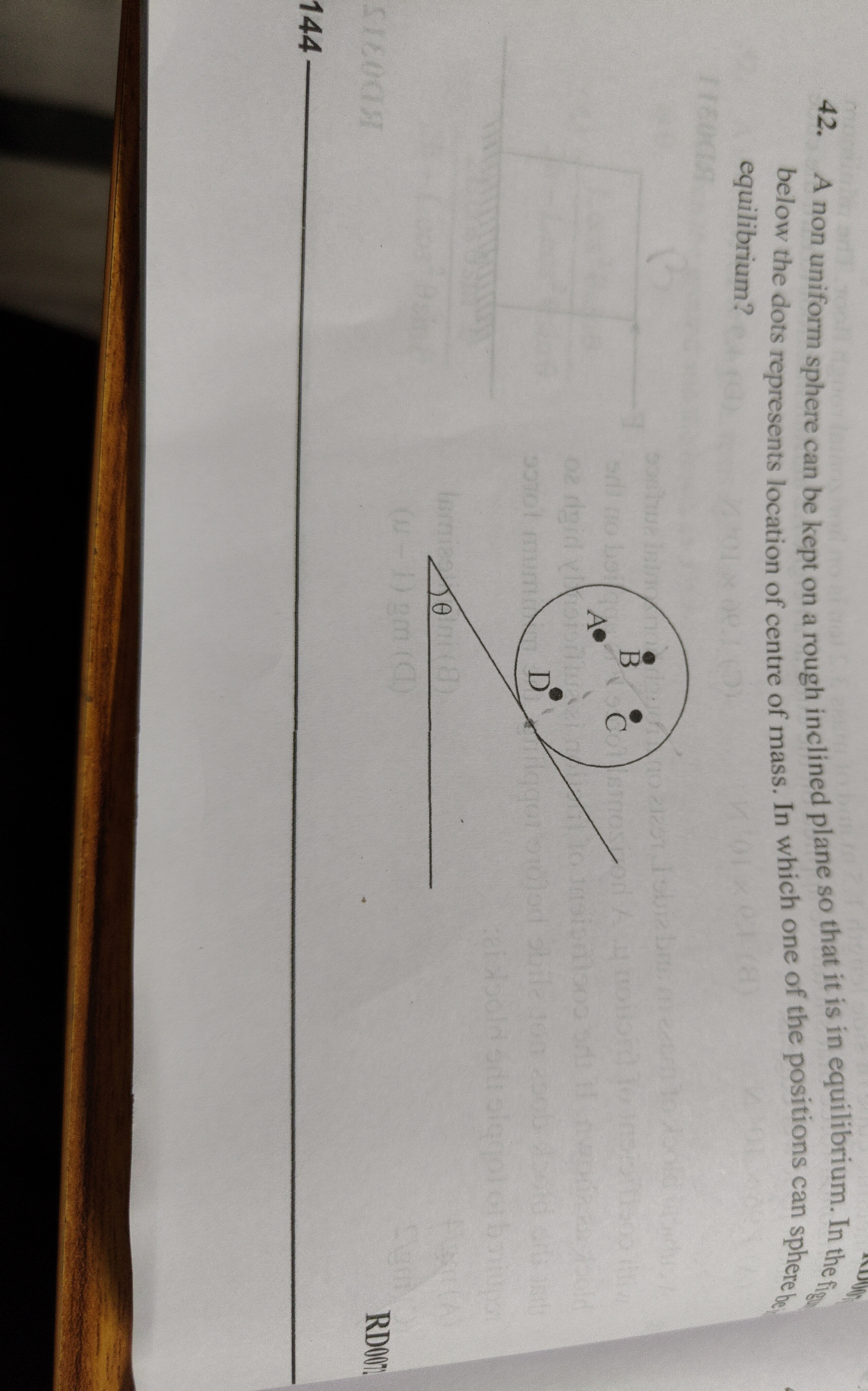
• A. A
• B. B
• C. C
• D. D

Answer 1

Answer: (D)

D

Answer 2

For a non-uniform sphere to be in equilibrium on a rough inclined plane, two conditions must be met:

1. Translational Equilibrium: The net force acting on the sphere must be zero. This implies that the component of gravity along the incline (mg sinθ) must be balanced by the static friction force (f_s), and the component of gravity perpendicular to the incline (mg cosθ) must be balanced by the normal force (N). So, f_s = mg sinθ and N = mg cosθ. For no sliding, f_s ≤ μ_s N, which means mg sinθ ≤ μ_s mg cosθ, or tanθ ≤ μ_s. This condition prevents the sphere from sliding down.
2. Rotational Equilibrium: The net torque acting on the sphere must be zero. It is convenient to calculate the torque about the point of contact (P) between the sphere and the inclined plane.
   • The normal force (N) acts through the point of contact P, so its torque about P is zero.
   • The friction force (f_s) also acts through the point of contact P, so its torque about P is zero.
   • The only remaining force is gravity (weight mg), which acts vertically downwards through the center of mass (CM). For the sphere to be in rotational equilibrium (i.e., not roll), the torque due to mg about P must be zero. This implies that the line of action of the weight mg must pass through the point of contact P.

Since the weight mg acts vertically downwards, the condition that its line of action passes through P means that the center of mass (CM) must be located vertically above the point of contact P.

Let's identify the point of contact (P) in the given figure. It is the lowest point of the sphere where it touches the inclined plane. Now, draw a vertical line passing through this point of contact P. We need to find which of the given points (A, B, C, D) lies on this vertical line.

Upon careful observation of the diagram:

• Points A, B, and C are located such that a vertical line drawn from them would not pass through the point of contact P. If the CM were at A, B, or C, the weight would create a net torque about P, causing the sphere to roll.
• Point D is located at the bottom-right portion of the sphere. If we draw a vertical line from the point of contact P, point D appears to lie on this vertical line. This means that if the center of mass is at D, the line of action of gravity passes directly through the point of contact P, resulting in zero torque about P.

Therefore, for the sphere to be in equilibrium, its center of mass must be at position D.