Question
Question: The integral $\int \frac{(1-\frac{1}{\sqrt{3}})(\cos x - \sin x)}{1+\frac{2}{\sqrt{3}}\sin 2x} dx$ i...
The integral ∫1+32sin2x(1−31)(cosx−sinx)dx is equal to:
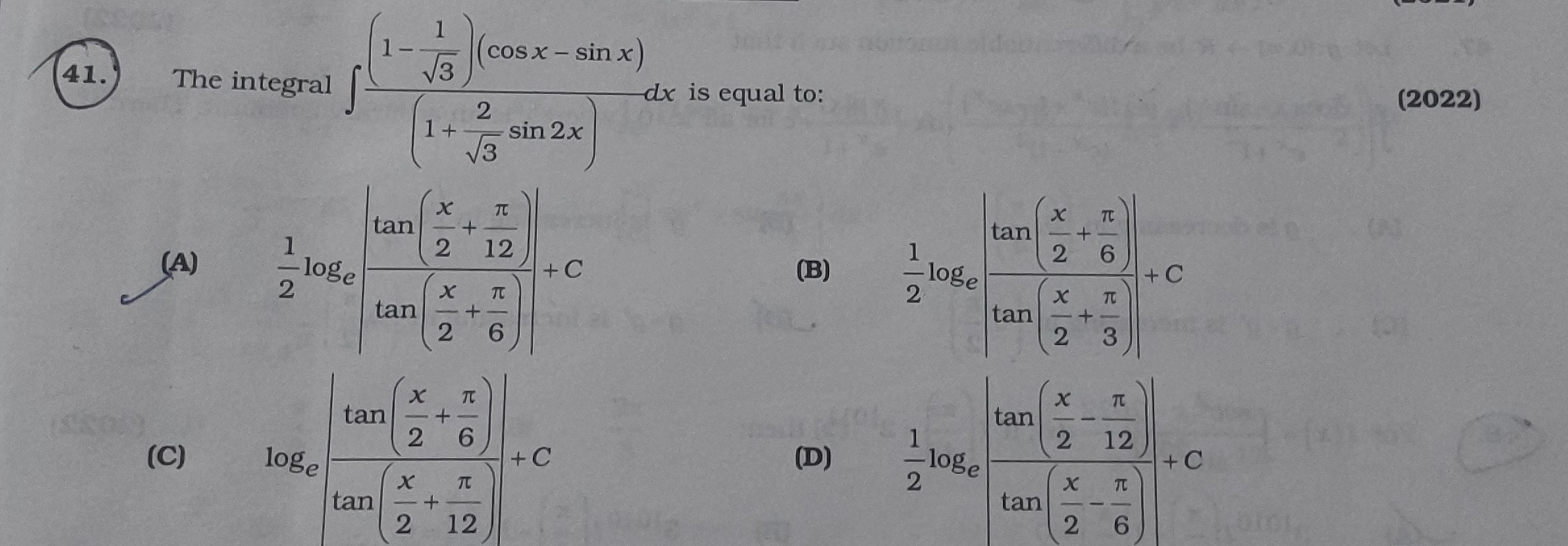
21logetan(2x+6π)tan(2x+12π)+C
21logetan(2x+3π)tan(2x+6π)+C
logetan(2x+12π)tan(2x+6π)+C
21logetan(2x−6π)tan(2x−12π)+C
21logetan(2x+6π)tan(2x+12π)+C
Solution
The given integral is I=∫1+32sin2x(1−31)(cosx−sinx)dx.
First, simplify the constant term: 1−31=33−1. So, I=33−1∫1+32sin2xcosx−sinxdx.
Let's use the substitution t=sinx+cosx. Then, dt=(cosx−sinx)dx. Also, t2=(sinx+cosx)2=sin2x+cos2x+2sinxcosx=1+sin2x. From this, sin2x=t2−1.
Substitute these into the integral: I=33−1∫1+32(t2−1)dt I=33−1∫33+2(t2−1)dt I=(3−1)∫3+2t2−2dt I=(3−1)∫2t2+(3−2)dt Factor out 2 from the denominator: I=23−1∫t2+23−2dt We can rewrite 23−2 as −22−3. I=23−1∫t2−22−3dt Notice that 22−3=44−23=4(3−1)2. So, let a2=4(3−1)2, which means a=23−1. The integral is of the form ∫x2−a2dx=2a1logx+ax−a+C. I=23−1⋅2a1logt+at−a+C I=23−1⋅2⋅23−11logt+23−1t−23−1+C I=23−1⋅3−11log2t+(3−1)2t−(3−1)+C I=21log2t+(3−1)2t−(3−1)+C.
Now, substitute back t=sinx+cosx. I=21log2(sinx+cosx)+(3−1)2(sinx+cosx)−(3−1)+C.
To match the options, we need to convert this expression into terms of tan(2x+α). We know that sinx+cosx=2sin(x+4π).
After applying sum-to-product formulas and simplifying, we get:
I=21logtan(2x+6π)tan(2x+12π)+C.
This matches option (A).
