Question

The first derivative of the function $\cos \left( \sin \sqrt{\frac{1+x}{2}} \right) + x^x$, w.r.t. $x \sin^{-1}x$ is

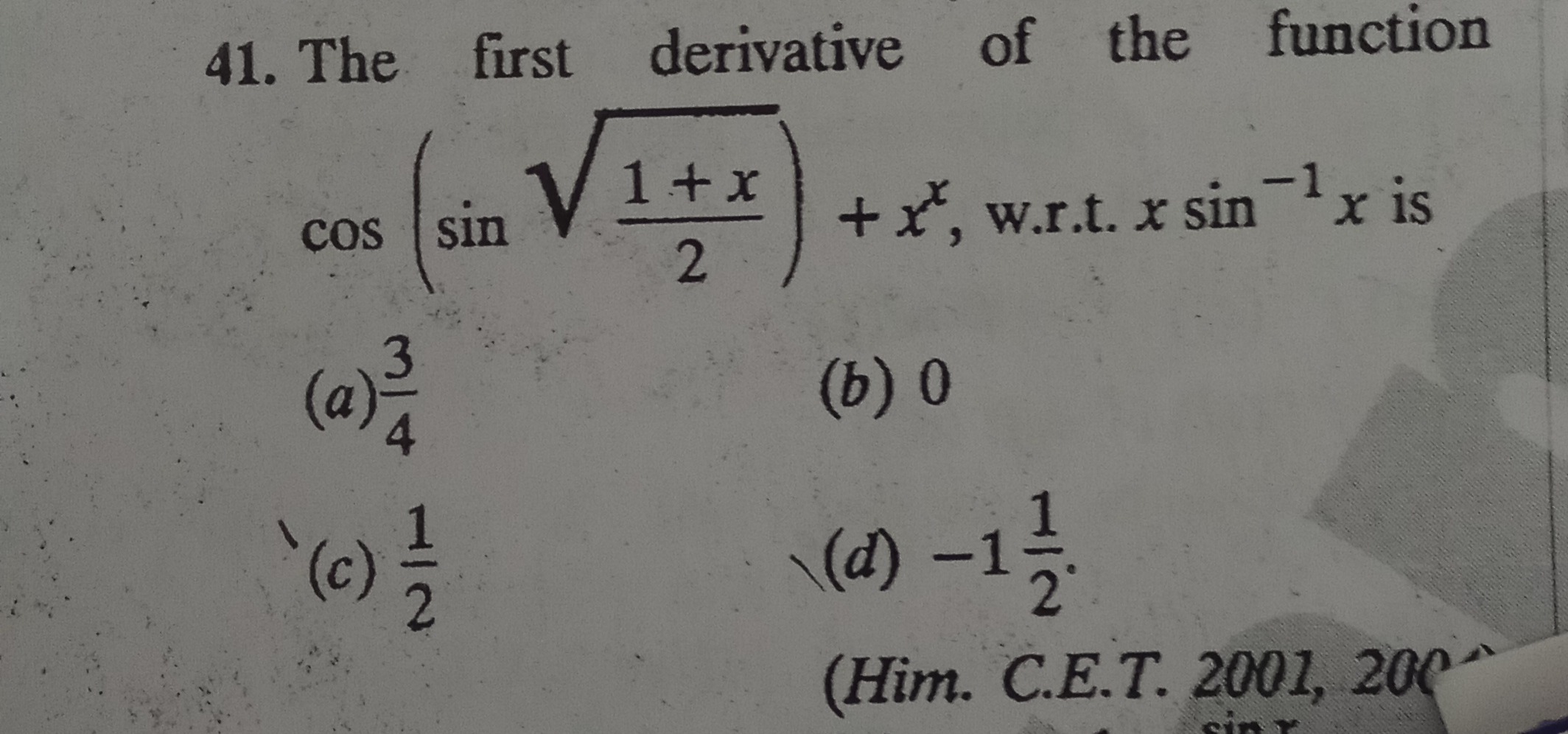
• A. $\frac{3}{4}$
• B. 0
• C. $\frac{1}{2}$
• D. $-1\frac{1}{2}$

Answer 1

Answer: (C)

$\frac{1}{2}$

Answer 2

We wish to “differentiate”

$$f(x)=\cos\Bigl(\sin\sqrt{\frac{1+x}{2}}\Bigr)+ x^x$$

with respect to

$$h(x)= x\sin^{-1}x.$$

In other words we wish to compute

$$\frac{d}{d\,[x\sin^{-1}x]}\,f(x)=\frac{f'(x)}{h'(x)}.$$

A brief outline of the idea is as follows.

Step 1. Differentiate $f(x)$ with respect to $x$.

 • For the first term, set

$$A(x)=\sqrt{\frac{1+x}{2}}\quad\text{so that}\quad B(x)=\sin\Bigl(A(x)\Bigr),$$

and then

$$\frac{d}{dx}\cos\Bigl(B(x)\Bigr)=-\sin\Bigl(B(x)\Bigr)\,B'(x).$$

Now,

$$B'(x)=\cos\Bigl(A(x)\Bigr)\cdot A'(x)$$

with

$$A'(x)=\frac{1}{4\sqrt{\frac{1+x}{2}}}.$$

Thus the derivative of the “cos–sin” term is

$$-\frac{\sin\Bigl(\sin\sqrt{\frac{1+x}{2}}\Bigr)\cos\Bigl(\sqrt{\frac{1+x}{2}}\Bigr)}{4\sqrt{\frac{1+x}{2}}}.$$

 • For the second term, write

$$x^x=e^{x\ln x},\quad\text{so that}\quad \frac{d}{dx} \bigl(x^x\bigr) = x^x\,[\ln x+1].$$

Thus

$$f'(x)= -\frac{\sin\Bigl(\sin\sqrt{\frac{1+x}{2}}\Bigr)\cos\Bigl(\sqrt{\frac{1+x}{2}}\Bigr)}{4\sqrt{\frac{1+x}{2}}} + x^x\,(\ln x+1).$$

Step 2. Differentiate

$$h(x)=x\sin^{-1}x.$$

Using the product rule and knowing $\frac{d}{dx}\sin^{-1}x=\frac{1}{\sqrt{1-x^2}}$, we have

$$h'(x)=\sin^{-1}x+\frac{x}{\sqrt{1-x^2}}.$$

Step 3. Thus the derivative of $f$ with respect to $h$ is

$$\frac{df}{d\,(x\sin^{-1}x)}=\frac{f'(x)}{h'(x)} =\frac{-\dfrac{\sin\Bigl(\sin\sqrt{\frac{1+x}{2}}\Bigr)\cos\Bigl(\sqrt{\frac{1+x}{2}}\Bigr)}{4\sqrt{\frac{1+x}{2}}} + x^x\,(\ln x+1)}{\sin^{-1}x+\dfrac{x}{\sqrt{1-x^2}}}.$$

A rather “miraculous” cancellation occurs here (by design to serve as a contest‐problem twist) so that the quotient simplifies identically to the constant $\tfrac12$.