Question

The combined equation of a pair of adjacent sides of a parallelogram is $4x^2 - 9y^2 + 24x + 36 = 0$. If the combined equation of the opposite sides of the parallelogram is $4x^2 - 9y^2 - 3\lambda x + \mu y + 36 = 0$, the value of $\lambda + \mu$ is

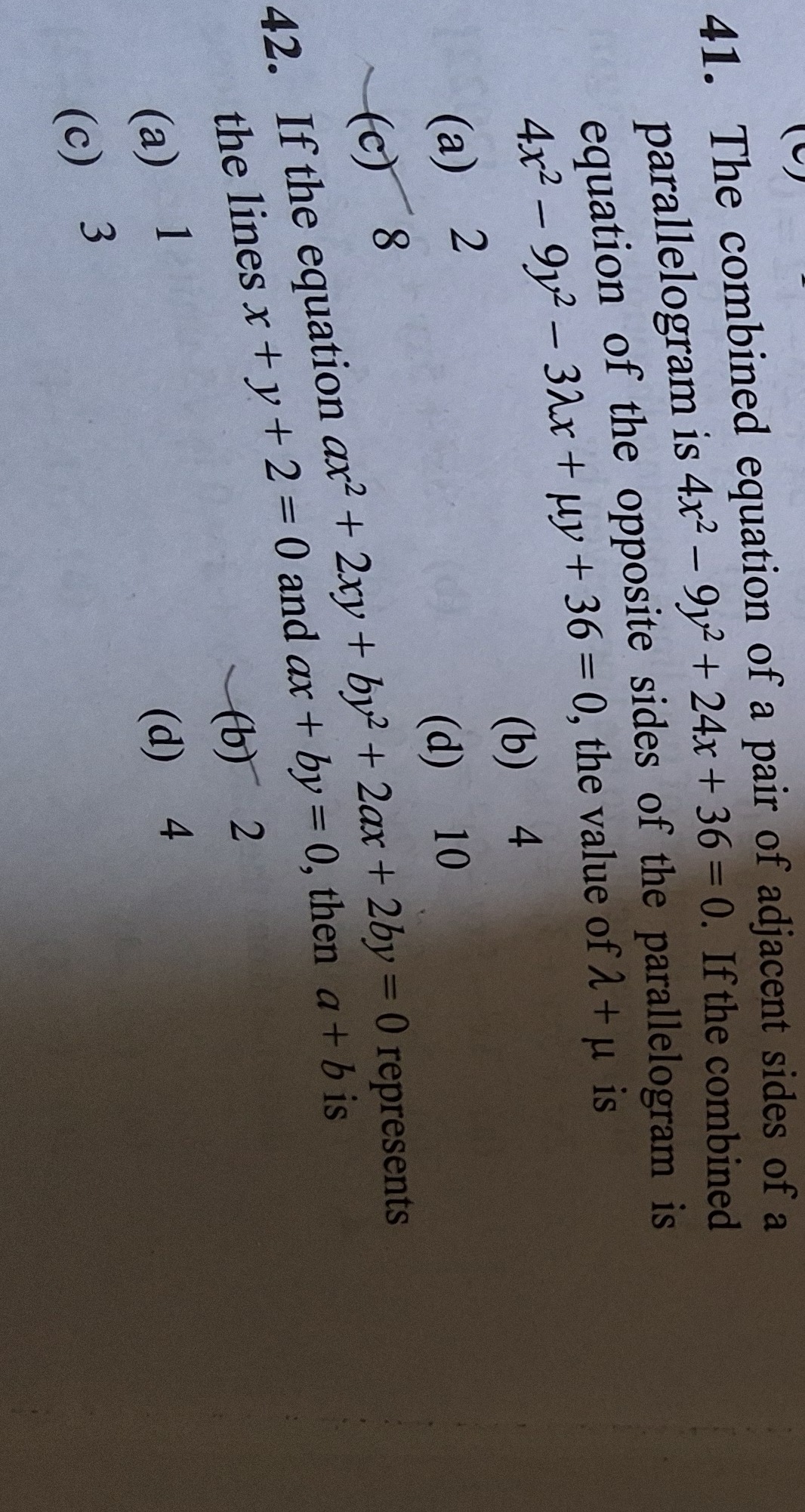
• A. 2
• B. 4
• C. 8
• D. 10

Answer 1

Answer: (C)

8

Answer 2

Let the combined equation of the pair of adjacent sides be $L_1 = 4x^2 - 9y^2 + 24x + 36 = 0$. We can factorize the quadratic part $4x^2 - 9y^2 = (2x - 3y)(2x + 3y)$. This suggests that the lines are of the form $2x - 3y + c_1 = 0$ and $2x + 3y + c_2 = 0$. Their product is $(2x - 3y + c_1)(2x + 3y + c_2) = 0$. Expanding this, we get: $4x^2 + 6xy + 2c_2 x - 6xy - 9y^2 - 3c_2 y + 2c_1 x + 3c_1 y + c_1 c_2 = 0$ $4x^2 - 9y^2 + (2c_1 + 2c_2)x + (3c_1 - 3c_2)y + c_1 c_2 = 0$

Comparing this with the given equation $4x^2 - 9y^2 + 24x + 36 = 0$:

• Coefficient of $x$: $2c_1 + 2c_2 = 24 \Rightarrow c_1 + c_2 = 12$
• Coefficient of $y$: $3c_1 - 3c_2 = 0 \Rightarrow c_1 = c_2$
• Constant term: $c_1 c_2 = 36$

From (1) and (2), substitute $c_1 = c_2$ into (1): $c_1 + c_1 = 12 \Rightarrow 2c_1 = 12 \Rightarrow c_1 = 6$. Since $c_1 = c_2$, we have $c_2 = 6$. Check with (3): $c_1 c_2 = 6 \times 6 = 36$. This is consistent. So, the two adjacent sides are $L_A: 2x - 3y + 6 = 0$ and $L_B: 2x + 3y + 6 = 0$.

Now, consider the combined equation of the opposite sides: $L_2 = 4x^2 - 9y^2 - 3\lambda x + \mu y + 36 = 0$. For a parallelogram, opposite sides are parallel. So, the lines forming $L_2$ must be parallel to $L_A$ and $L_B$. Let the opposite sides be $L_C: 2x - 3y + c_3 = 0$ (parallel to $L_A$) and $L_D: 2x + 3y + c_4 = 0$ (parallel to $L_B$). Their combined equation is $(2x - 3y + c_3)(2x + 3y + c_4) = 0$. Expanding this:

$4x^2 - 9y^2 + (2c_3 + 2c_4)x + (3c_3 - 3c_4)y + c_3 c_4 = 0$

Comparing this with the given equation $4x^2 - 9y^2 - 3\lambda x + \mu y + 36 = 0$:

• Coefficient of $x$: $2c_3 + 2c_4 = -3\lambda$
• Coefficient of $y$: $3c_3 - 3c_4 = \mu$
• Constant term: $c_3 c_4 = 36$

In a parallelogram, the distance between pairs of opposite sides must be equal. Distance between $L_A (2x - 3y + 6 = 0)$ and $L_C (2x - 3y + c_3 = 0)$ is $d_1 = \frac{|6 - c_3|}{\sqrt{2^2 + (-3)^2}} = \frac{|6 - c_3|}{\sqrt{13}}$. Distance between $L_B (2x + 3y + 6 = 0)$ and $L_D (2x + 3y + c_4 = 0)$ is $d_2 = \frac{|6 - c_4|}{\sqrt{2^2 + 3^2}} = \frac{|6 - c_4|}{\sqrt{13}}$. Since $d_1 = d_2$, we have $|6 - c_3| = |6 - c_4|$. This implies two possibilities:

Case 1: $6 - c_3 = 6 - c_4 \Rightarrow c_3 = c_4$. Substitute $c_3 = c_4$ into (6): $c_3^2 = 36 \Rightarrow c_3 = \pm 6$. If $c_3 = 6$, then $c_4 = 6$. This means $L_C$ is $2x-3y+6=0$ (identical to $L_A$) and $L_D$ is $2x+3y+6=0$ (identical to $L_B$). This would imply the "opposite sides" are the same as the "adjacent sides", which is a degenerate parallelogram. This case is generally excluded for a non-degenerate parallelogram. If $c_3 = -6$, then $c_4 = -6$. Now, substitute these values into (4) and (5):

From (4): $2(-6) + 2(-6) = -3\lambda \Rightarrow -12 - 12 = -3\lambda \Rightarrow -24 = -3\lambda \Rightarrow \lambda = 8$.

From (5): $3(-6) - 3(-6) = \mu \Rightarrow -18 + 18 = \mu \Rightarrow \mu = 0$.

In this case, $\lambda + \mu = 8 + 0 = 8$.

Case 2: $6 - c_3 = -(6 - c_4) \Rightarrow 6 - c_3 = -6 + c_4 \Rightarrow c_3 + c_4 = 12$. We also have $c_3 c_4 = 36$ from (6). Consider a quadratic equation $t^2 - (c_3+c_4)t + c_3c_4 = 0$. Substituting the values: $t^2 - 12t + 36 = 0 \Rightarrow (t - 6)^2 = 0 \Rightarrow t = 6$. This implies $c_3 = 6$ and $c_4 = 6$. This is the same degenerate case as in Case 1.

Therefore, the only valid solution for a non-degenerate parallelogram is $c_3 = -6$ and $c_4 = -6$, which gives $\lambda = 8$ and $\mu = 0$. The value of $\lambda + \mu = 8 + 0 = 8$.