Question
Question: If y = cos (sin x²), then at x = $\sqrt{\frac{\pi}{2}}$, $\frac{dy}{dx}$ =...
If y = cos (sin x²), then at x = 2π, dxdy =
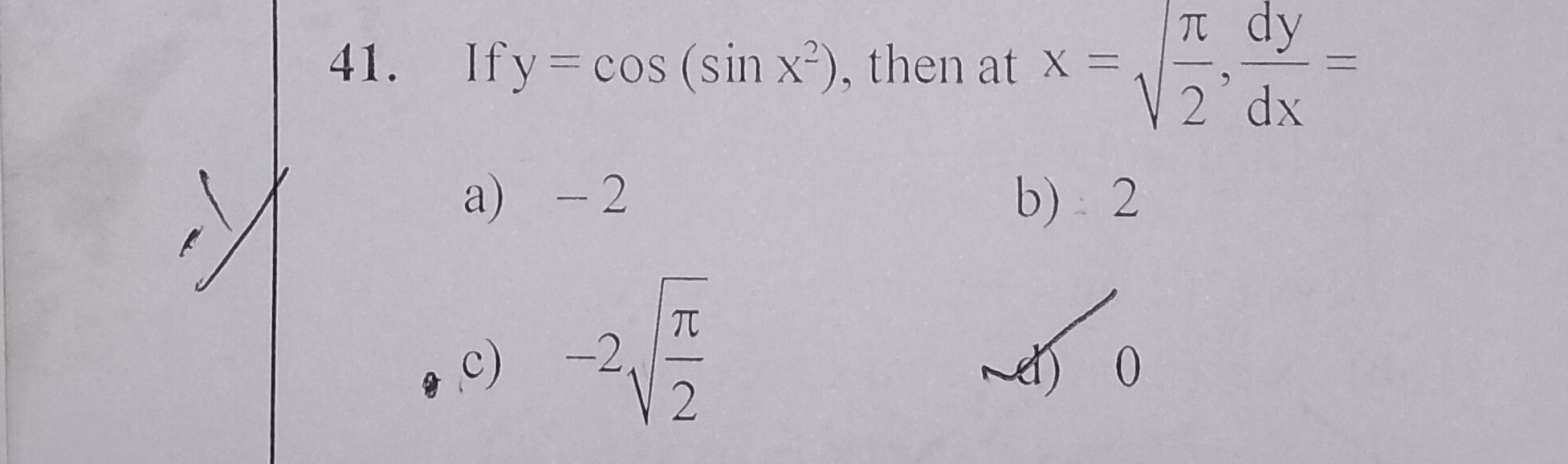
A
- 2
B
2
C
-22π
D
0
Answer
0
Explanation
Solution
Given:
y=cos(sin(x2))Differentiate using the chain rule:
dxdy=−sin(sinx2)⋅cos(x2)⋅dxd(x2)Since dxd(x2)=2x, we have:
dxdy=−2xcos(x2)sin(sinx2)At x=2π,
x2=2πandcos(2π)=0.Thus,
dxdy=−22π⋅0⋅sin(sin2π)=0.