Question
Question: If log(x + y) = 2xy, then $\frac{dy}{dx}$ at x = 0 is...
If log(x + y) = 2xy, then dxdy at x = 0 is
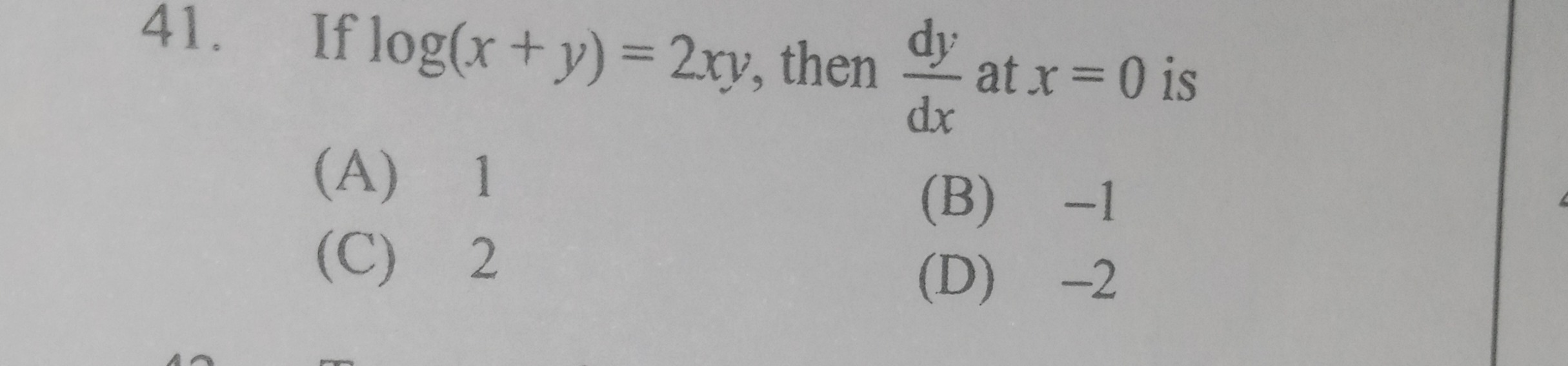
1
-1
2
-2
1
Solution
Given the equation log(x+y)=2xy.
We need to find dxdy at x=0.
First, find the value of y when x=0. Substitute x=0 into the given equation:
log(0+y)=2(0)y
log(y)=0
Since log(y)=0 implies y=e0, we have y=1.
So, we need to find dxdy at the point (x,y)=(0,1).
Next, differentiate the given equation implicitly with respect to x.
dxd(log(x+y))=dxd(2xy)
Using the chain rule on the left side:
x+y1⋅dxd(x+y)=x+y1(1+dxdy)
Using the product rule on the right side:
dxd(2xy)=2⋅dxd(xy)=2(1⋅y+x⋅dxdy)=2y+2xdxdy
Equating the derivatives of both sides:
x+y1(1+dxdy)=2y+2xdxdy
Now, we need to find the value of dxdy at the point (0,1). Substitute x=0 and y=1 into the differentiated equation:
0+11(1+dxdy(0,1))=2(1)+2(0)dxdy(0,1)
11(1+dxdy(0,1))=2+0
1(1+dxdy(0,1))=2
1+dxdy(0,1)=2
dxdy(0,1)=2−1
dxdy(0,1)=1
Thus, the value of dxdy at x=0 is 1.
