Question

If $A=\begin{bmatrix}0 & -\tan \alpha/2\\\tan \alpha/2 & 0\end{bmatrix}$ and $I$ is a 2×2 unit matrix, then $(I-A)\begin{bmatrix}\cos \alpha & -\sin \alpha\\\sin \alpha & \cos \alpha\end{bmatrix}=I+kA.$ The value of k is

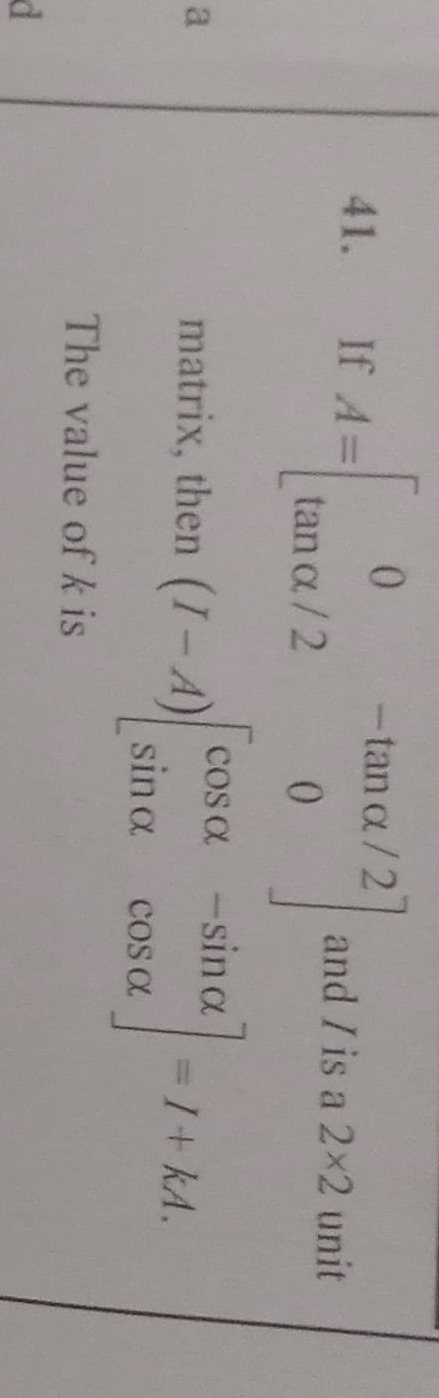
• A. -1
• B. 1
• C. 2
• D. None of these

Answer 1

Answer: (B)

1

Answer 2

Let $t = \tan \alpha/2$. Then $A = \begin{bmatrix} 0 & -t \\ t & 0 \end{bmatrix}$. Also, $\cos \alpha = \frac{1-t^2}{1+t^2}$ and $\sin \alpha = \frac{2t}{1+t^2}$.

Then

$I - A = \begin{bmatrix} 1 & t \\ -t & 1 \end{bmatrix}$.

Also, let $M = \begin{bmatrix} \cos \alpha & - \sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix} = \begin{bmatrix} \frac{1-t^2}{1+t^2} & - \frac{2t}{1+t^2} \\ \frac{2t}{1+t^2} & \frac{1-t^2}{1+t^2} \end{bmatrix}$.

Then $(I-A)M = \begin{bmatrix} 1 & t \\ -t & 1 \end{bmatrix} \begin{bmatrix} \frac{1-t^2}{1+t^2} & - \frac{2t}{1+t^2} \\ \frac{2t}{1+t^2} & \frac{1-t^2}{1+t^2} \end{bmatrix} = \frac{1}{1+t^2} \begin{bmatrix} 1-t^2 + 2t^2 & -2t + t - t^3 \\ -t + t^3 + 2t & 2t^2 + 1 - t^2 \end{bmatrix} = \frac{1}{1+t^2} \begin{bmatrix} 1+t^2 & -t(1+t^2) \\ t(1+t^2) & 1+t^2 \end{bmatrix} = \begin{bmatrix} 1 & -t \\ t & 1 \end{bmatrix}$.

Also, $I + kA = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} + k \begin{bmatrix} 0 & -t \\ t & 0 \end{bmatrix} = \begin{bmatrix} 1 & -kt \\ kt & 1 \end{bmatrix}$.

Therefore, $\begin{bmatrix} 1 & -t \\ t & 1 \end{bmatrix} = \begin{bmatrix} 1 & -kt \\ kt & 1 \end{bmatrix}$, so $k=1$.