Question

H₂ and O₂ are kept in mass ratio 1 : 8 respectively at 6 atm. If small orifice is made, then moles of H₂ with respect to O₂ coming out initially, is

Answer 1

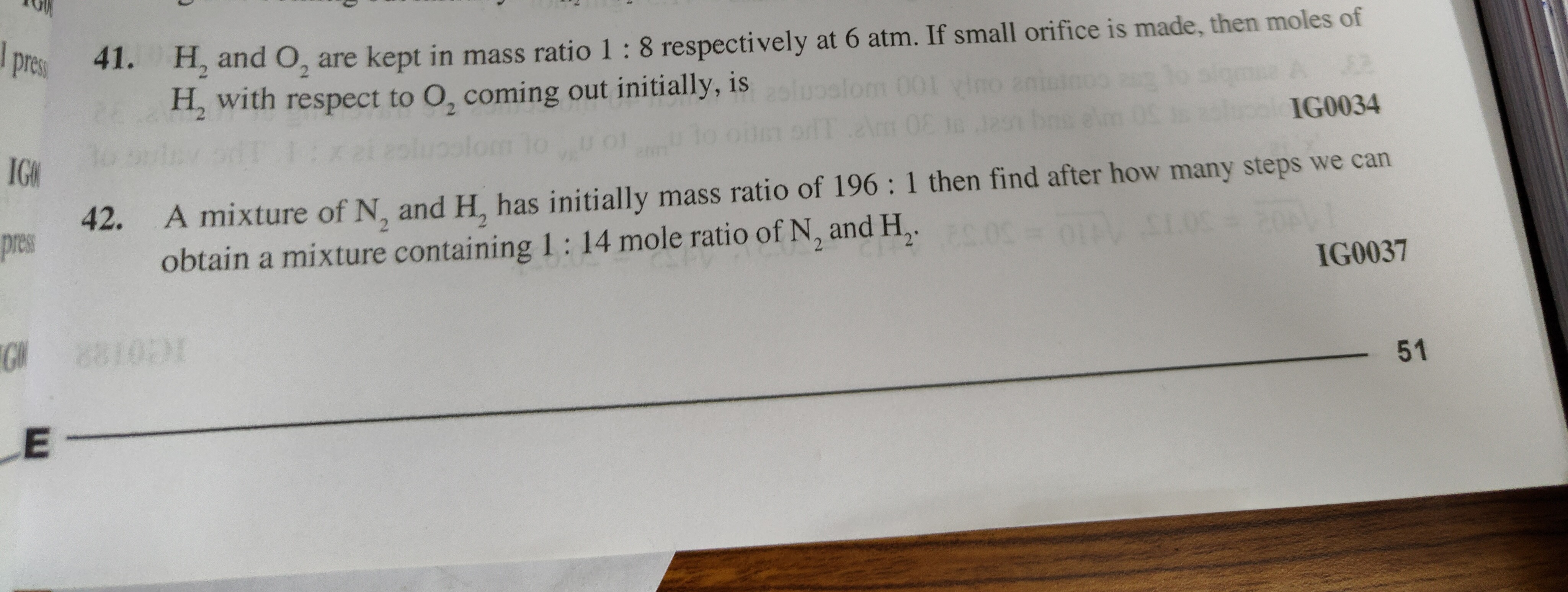
8:1

Answer 2

1. Calculate Molar Masses:

   • Molar mass of H₂ ($M_{H_2}$) = 2 g/mol
   • Molar mass of O₂ ($M_{O_2}$) = 32 g/mol

2. Determine Initial Mole Ratio: Let the mass of H₂ be $m_{H_2} = x$ and the mass of O₂ be $m_{O_2} = 8x$.

   • Number of moles of H₂ ($n_{H_2}$) = $m_{H_2} / M_{H_2} = x / 2$
   • Number of moles of O₂ ($n_{O_2}$) = $m_{O_2} / M_{O_2} = 8x / 32 = x / 4$ The initial mole ratio is $n_{H_2} : n_{O_2} = (x/2) : (x/4) = 2 : 1$.

3. Calculate Partial Pressures: The total pressure ($P_{total}$) is 6 atm.

   • Mole fraction of H₂ ($X_{H_2}$) = $n_{H_2} / (n_{H_2} + n_{O_2}) = (x/2) / (x/2 + x/4) = (x/2) / (3x/4) = 2/3$.
   • Mole fraction of O₂ ($X_{O_2}$) = $n_{O_2} / (n_{H_2} + n_{O_2}) = (x/4) / (3x/4) = 1/3$.
   • Partial pressure of H₂ ($P_{H_2}$) = $X_{H_2} \times P_{total} = (2/3) \times 6 \text{ atm} = 4 \text{ atm}$.
   • Partial pressure of O₂ ($P_{O_2}$) = $X_{O_2} \times P_{total} = (1/3) \times 6 \text{ atm} = 2 \text{ atm}$.

4. Apply Graham's Law of Effusion: The rate of effusion of a gas through a small orifice is proportional to its partial pressure and inversely proportional to the square root of its molar mass. Rate $\propto \frac{P}{\sqrt{M}}$ The ratio of moles coming out initially is equal to the ratio of their rates of effusion. $\frac{\text{Moles of H₂ coming out}}{\text{Moles of O₂ coming out}} = \frac{\text{Rate of H₂}}{\text{Rate of O₂}} = \frac{P_{H_2}}{P_{O_2}} \sqrt{\frac{M_{O_2}}{M_{H_2}}}$ $\frac{\text{Moles of H₂ coming out}}{\text{Moles of O₂ coming out}} = \frac{4 \text{ atm}}{2 \text{ atm}} \sqrt{\frac{32 \text{ g/mol}}{2 \text{ g/mol}}}$ $\frac{\text{Moles of H₂ coming out}}{\text{Moles of O₂ coming out}} = 2 \sqrt{16} = 2 \times 4 = 8$ The moles of H₂ with respect to O₂ coming out initially is 8:1.