Question

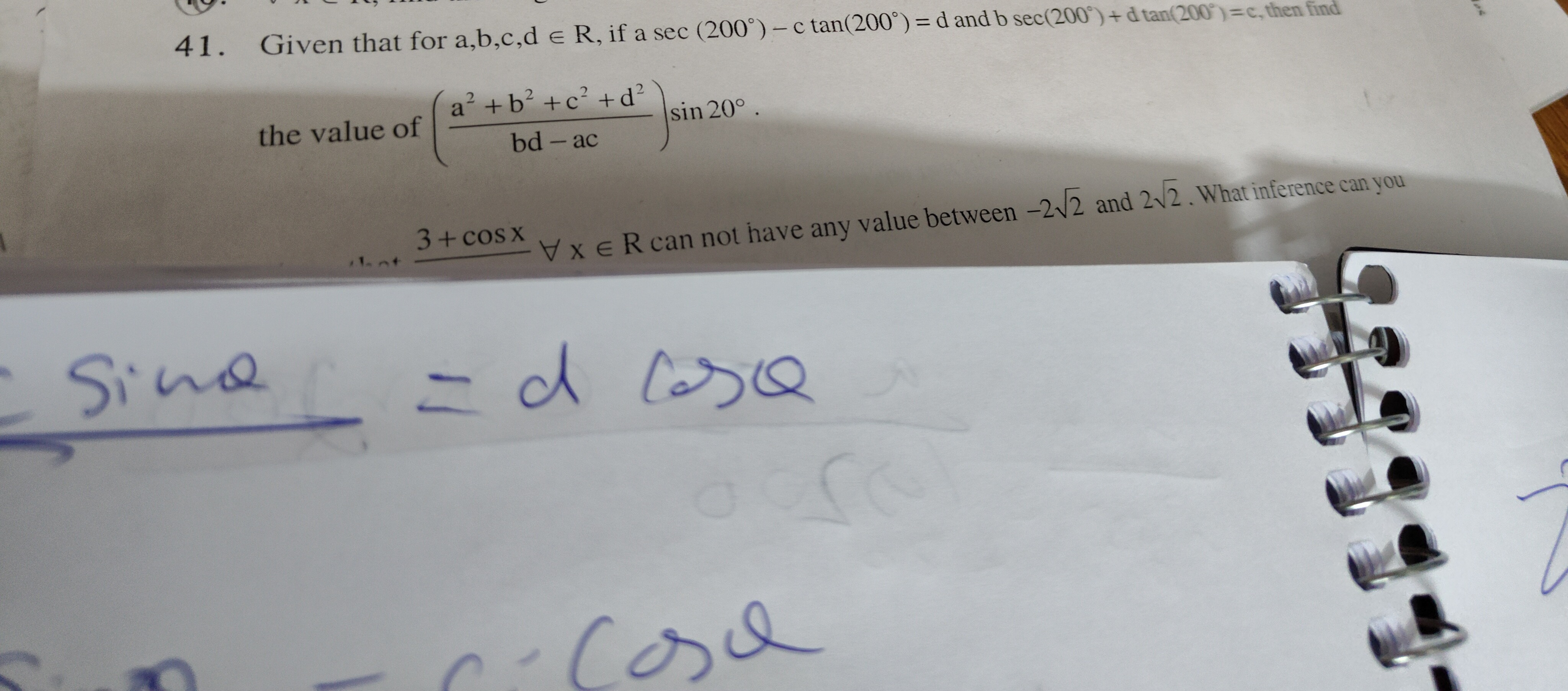
Given that for a,b,c,d ∈ R, if a sec (200°) - c tan(200°) = d and b sec(200°) + d tan(200°)=c, then find the value of $\left(\frac{a^2 + b^2+c^2 + d^2}{bd - ac}\right)$ sin 20°.

Answer 1

2

Answer 2

The problem requires us to evaluate an expression involving variables a, b, c, d, which are related by two given trigonometric equations.

Let the given equations be:

1. $a \sec (200^\circ) - c \tan(200^\circ) = d$
2. $b \sec(200^\circ) + d \tan(200^\circ) = c$

Let $x = 200^\circ$. The equations become:

1. $a \sec x - c \tan x = d$
2. $b \sec x + d \tan x = c$

Multiply both equations by $\cos x$ to simplify them:

1. $a - c \sin x = d \cos x \implies a = d \cos x + c \sin x$ (Equation A)
2. $b + d \sin x = c \cos x \implies b = c \cos x - d \sin x$ (Equation B)

Now, we need to evaluate the expression $\left(\frac{a^2 + b^2+c^2 + d^2}{bd - ac}\right) \sin 20^\circ$.

First, let's calculate $a^2 + b^2$: $a^2 = (d \cos x + c \sin x)^2 = d^2 \cos^2 x + c^2 \sin^2 x + 2cd \cos x \sin x$ $b^2 = (c \cos x - d \sin x)^2 = c^2 \cos^2 x + d^2 \sin^2 x - 2cd \cos x \sin x$

Adding $a^2$ and $b^2$: $a^2 + b^2 = (d^2 \cos^2 x + c^2 \sin^2 x + 2cd \cos x \sin x) + (c^2 \cos^2 x + d^2 \sin^2 x - 2cd \cos x \sin x)$ $a^2 + b^2 = d^2 (\cos^2 x + \sin^2 x) + c^2 (\sin^2 x + \cos^2 x)$ Using the identity $\sin^2 x + \cos^2 x = 1$: $a^2 + b^2 = d^2(1) + c^2(1) = c^2 + d^2$.

Now, the numerator of the expression is $a^2 + b^2 + c^2 + d^2$: Numerator $= (c^2 + d^2) + c^2 + d^2 = 2(c^2 + d^2)$.

Next, let's calculate the denominator $bd - ac$: $ac = (d \cos x + c \sin x) c = cd \cos x + c^2 \sin x$ $bd = (c \cos x - d \sin x) d = cd \cos x - d^2 \sin x$

Subtracting $ac$ from $bd$: Denominator $= bd - ac = (cd \cos x - d^2 \sin x) - (cd \cos x + c^2 \sin x)$ Denominator $= cd \cos x - d^2 \sin x - cd \cos x - c^2 \sin x$ Denominator $= -d^2 \sin x - c^2 \sin x = -(c^2 + d^2) \sin x$.

Now, substitute the expressions for the numerator and the denominator into the fraction: $\frac{a^2 + b^2 + c^2 + d^2}{bd - ac} = \frac{2(c^2 + d^2)}{-(c^2 + d^2) \sin x}$ For this expression to be defined, $-(c^2 + d^2) \sin x \neq 0$. Since $x = 200^\circ$, $\sin(200^\circ) = \sin(180^\circ + 20^\circ) = -\sin(20^\circ) \neq 0$. Thus, we must have $c^2 + d^2 \neq 0$. Assuming $c^2 + d^2 \neq 0$, we can cancel the term $(c^2 + d^2)$: $\frac{a^2 + b^2 + c^2 + d^2}{bd - ac} = \frac{2}{-\sin x} = -2 \operatorname{cosec} x$

Now, substitute $x = 200^\circ$: $\frac{a^2 + b^2 + c^2 + d^2}{bd - ac} = -2 \operatorname{cosec}(200^\circ)$

Finally, we need to find the value of $\left(\frac{a^2 + b^2+c^2 + d^2}{bd - ac}\right) \sin 20^\circ$: Value $= (-2 \operatorname{cosec}(200^\circ)) \sin 20^\circ$ We know that $\operatorname{cosec}(200^\circ) = \frac{1}{\sin(200^\circ)}$. Value $= -2 \frac{1}{\sin(200^\circ)} \sin 20^\circ$

Recall the trigonometric identity for angles in the third quadrant: $\sin(180^\circ + \theta) = -\sin \theta$. So, $\sin(200^\circ) = \sin(180^\circ + 20^\circ) = -\sin(20^\circ)$.

Substitute this into the expression: Value $= -2 \frac{1}{-\sin(20^\circ)} \sin 20^\circ$ Value $= -2 \left(-\frac{1}{\sin(20^\circ)}\right) \sin 20^\circ$ Value $= 2 \frac{\sin(20^\circ)}{\sin(20^\circ)}$

Since $\sin(20^\circ) \neq 0$, we can cancel $\sin(20^\circ)$: Value $= 2$.

The second part of the question "3 + cosx ∀ x ∈ R can not have any value between -2√2 and 2√2. What inference can you" appears to be a separate, incomplete statement and is not related to the first part of the problem. Therefore, only the first part is addressed.

The final answer is $\boxed{2}$.

Explanation of the solution:

1. Rewrite the given equations using $x = 200^\circ$ and convert them from sec/tan to sin/cos by multiplying by $\cos x$. This yields $a = d \cos x + c \sin x$ and $b = c \cos x - d \sin x$.
2. Calculate $a^2 + b^2$ using the derived expressions for $a$ and $b$. This simplifies to $c^2 + d^2$.
3. The numerator of the fraction becomes $a^2 + b^2 + c^2 + d^2 = (c^2 + d^2) + c^2 + d^2 = 2(c^2 + d^2)$.
4. Calculate the denominator $bd - ac$ using the expressions for $a, b, c, d$. This simplifies to $-(c^2 + d^2) \sin x$.
5. Form the fraction $\frac{a^2 + b^2 + c^2 + d^2}{bd - ac} = \frac{2(c^2 + d^2)}{-(c^2 + d^2) \sin x}$. Assuming $c^2+d^2 \neq 0$, this simplifies to $\frac{2}{-\sin x} = -2 \operatorname{cosec} x$.
6. Substitute $x = 200^\circ$ into the simplified fraction: $-2 \operatorname{cosec}(200^\circ)$.
7. Multiply this result by $\sin 20^\circ$: $(-2 \operatorname{cosec}(200^\circ)) \sin 20^\circ$.
8. Use the identity $\operatorname{cosec}(200^\circ) = \frac{1}{\sin(200^\circ)}$ and the reduction formula $\sin(200^\circ) = \sin(180^\circ + 20^\circ) = -\sin(20^\circ)$.
9. The expression becomes $-2 \frac{1}{-\sin(20^\circ)} \sin 20^\circ = 2$.