Question

For a ∈ R (the set of all real numbers), a ≠ -1, $\lim_{n \to \infty} \frac{(1^a + 2^a + ... + n^a)}{(n+1)^{a-1}[(na+1)+(na+2)+...+(na+n)]} = \frac{1}{60}$.

Then a =

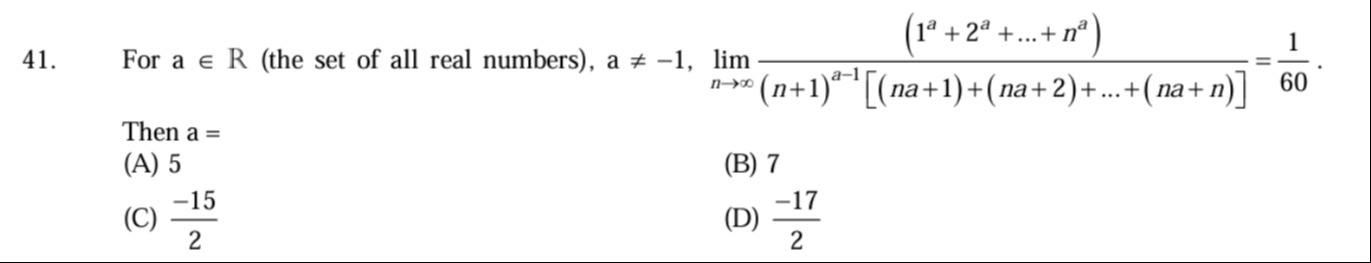
• A. 5
• B. 7
• C. $\frac{-15}{2}$
• D. $\frac{-17}{2}$

Answer 1

Answer: (B)

7

Answer 2

We are given:

$$\lim_{n\to\infty}\frac{1^a+2^a+\cdots+n^a}{(n+1)^{a-1}\Bigl[(na+1)+(na+2)+\cdots+(na+n)\Bigr]}=\frac{1}{60}.$$

1. Numerator Evaluation:
   For large $n$, using integral approximation:

   $$\sum_{k=1}^{n} k^a \sim \frac{n^{a+1}}{a+1} \quad \text{(provided } a > -1\text{)}.$$

2. Denominator Evaluation:
   First, note that:

   $$\sum_{j=1}^{n} (na + j) = na\cdot n + \frac{n(n+1)}{2} \sim n^2\left(a+\frac{1}{2}\right).$$

   Also, $(n+1)^{a-1} \sim n^{a-1}$. Thus, the denominator behaves as:

   $$n^{a-1}\cdot n^2\left(a+\frac{1}{2}\right)= n^{a+1}\left(a+\frac{1}{2}\right).$$

3. Taking the Limit:
   The $n^{a+1}$ factors cancel:

   $$\lim_{n\to\infty}\frac{\frac{n^{a+1}}{a+1}}{n^{a+1}\left(a+\frac{1}{2}\right)} = \frac{1}{(a+1)\left(a+\frac{1}{2}\right)}=\frac{1}{60}.$$

   Therefore,

   $$(a+1)\left(a+\frac{1}{2}\right)=60.$$

4. Solve the Equation:
   Expand:

   $$a^2+\frac{3}{2}a+\frac{1}{2}=60 \quad \Longrightarrow \quad a^2+\frac{3}{2}a-\frac{119}{2}=0.$$

   Multiply through by 2:

   $$2a^2+3a-119=0.$$

   Using the quadratic formula:

   $$a=\frac{-3\pm\sqrt{3^2-4\cdot 2\cdot(-119)}}{2\cdot 2}=\frac{-3\pm\sqrt{9+952}}{4}=\frac{-3\pm\sqrt{961}}{4}.$$

   Since $\sqrt{961}=31$, the solutions are:

   $$a=\frac{-3+31}{4}=\frac{28}{4}=7 \quad \text{or} \quad a=\frac{-3-31}{4}=\frac{-34}{4}=-\frac{17}{2}.$$

5. Validity Check:
   The asymptotic approximation used (via an integral) is valid when $a>-1$. Hence, the solution $a=-\frac{17}{2}$ is extraneous.

Thus, the valid answer is $a=7$.