Question

$400$ students of class X of a school appeared in a test of $100$ marks in the subject of social studies and the data about the marks secured is as below :

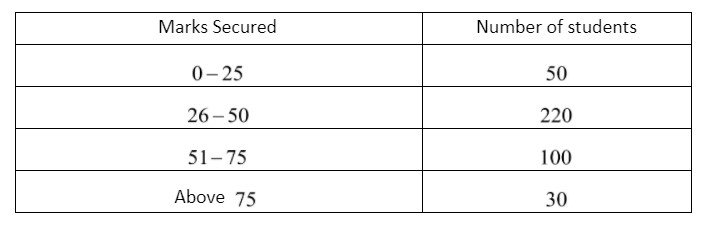
Total Number of students = $400$
If the result card of a student he picked up at random , what is the probability that the student has secured more than $50$ marks .
A) $0.586$
B) $0.75$
C) $0.325$
D) $0.1$

Answer 1

As for the probability of the student has secured more than $50$ marks is equal to the = $\dfrac{{{\text{Favourable outcomes }}}}{{{\text{Total number of outcomes }}}}$, So from the given data find the favorable outcomes i.e number of students who secured more than $50$ marks and find total number of outcomes i.e total number of students.Using probability formula we try to get the answer.

Complete step-by-step answer:
Probability is defined as the ratio of favorable outcomes to the total number of outcomes.
So, probability of an event is equal to the = $\dfrac{{{\text{Favourable outcomes }}}}{{{\text{Total number of outcomes }}}}$
In the given question it is asked that the probability that the student has secured more than $50$ marks .
Hence for this the number of students securing more than $50$ marks is favourable outcomes ,
Total number of students is total number outcomes that is $400$
So number of student scoring more than $50$ marks is $100 + 30$= $130$ ( we don't have to consider the student who score $50$ marks )
Favourable outcomes = $130$
and total number of outcomes is $400$
Now ,
Probability of the students who secure more than $50$ marks = $\dfrac{{130}}{{400}}$
On dividing $130$ to $400$ we get $0.325$

So, the correct answer is “Option C”.

Note: Probability of any event always lies between $0$ to $1$ . If your answer comes apart from this then cross check it.If in the question it is asked one additional thing that the probability of that the student has secured less than $50$ marks hence it is equal to
Probability of less than $50$ marks = $1$- Probability of scored more than $50$ marks