Question

Two chords are drawn from the point P(h, k) on the circle $x^2 + y^2 = hx + ky$. If the y-axis divides both the chords in the ratio 2:3, then which of the following may be correct?

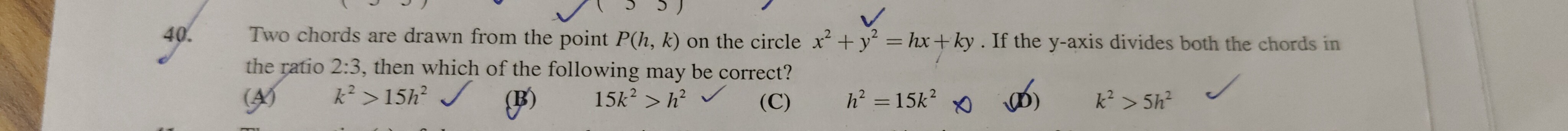
• A. $k^2 > 15h^2$
• B. $15k^2 > h^2$
• C. $h^2 = 15k^2$
• D. $k^2 > 5h^2$

Answer 1

Answer: (A)

$k^2 > 15h^2$

Answer 2

The circle equation is $x^2 + y^2 - hx - ky = 0$. The point $P(h, k)$ lies on the circle. Let the two chords drawn from $P$ be $PC_1$ and $PC_2$, where $C_1(x_1, y_1)$ and $C_2(x_2, y_2)$ are points on the circle.

The y-axis ($x=0$) divides chord $PC_1$ in the ratio 2:3. Let $Q_1$ be the point of division on the y-axis. Using the section formula, $Q_1 = \frac{3P + 2C_1}{2+3}$. The x-coordinate of $Q_1$ is $x_{Q_1} = \frac{3h + 2x_1}{5}$. Since $Q_1$ is on the y-axis, $x_{Q_1} = 0$. $\frac{3h + 2x_1}{5} = 0 \implies 3h + 2x_1 = 0 \implies x_1 = -\frac{3h}{2}$ Similarly, for chord $PC_2$, $x_2 = -\frac{3h}{2}$. Thus, both $C_1$ and $C_2$ must have an x-coordinate of $-\frac{3h}{2}$.

Since $C_1$ and $C_2$ lie on the circle $x^2 + y^2 - hx - ky = 0$, we substitute $x = -\frac{3h}{2}$: $\left(-\frac{3h}{2}\right)^2 + y^2 - h\left(-\frac{3h}{2}\right) - ky = 0$ $\frac{9h^2}{4} + y^2 + \frac{3h^2}{2} - ky = 0$ $y^2 - ky + \left(\frac{9h^2}{4} + \frac{6h^2}{4}\right) = 0$ $y^2 - ky + \frac{15h^2}{4} = 0$ For two distinct points $C_1$ and $C_2$ to exist on the circle with $x = -\frac{3h}{2}$ (which implies two distinct chords), this quadratic equation for $y$ must have two distinct real roots. The discriminant $D$ must be positive: $D = (-k)^2 - 4(1)\left(\frac{15h^2}{4}\right) > 0$ $k^2 - 15h^2 > 0$ $k^2 > 15h^2$