Question
Question: The value of $F(x) = 6\cos x\sqrt{1+\tan^2x} + 2\sin x\sqrt{1+\cot^2x}$, Where $x \in (0, 2\pi) - ...
The value of
F(x)=6cosx1+tan2x+2sinx1+cot2x,
Where x∈(0,2π)−{π,2π,23π} may be
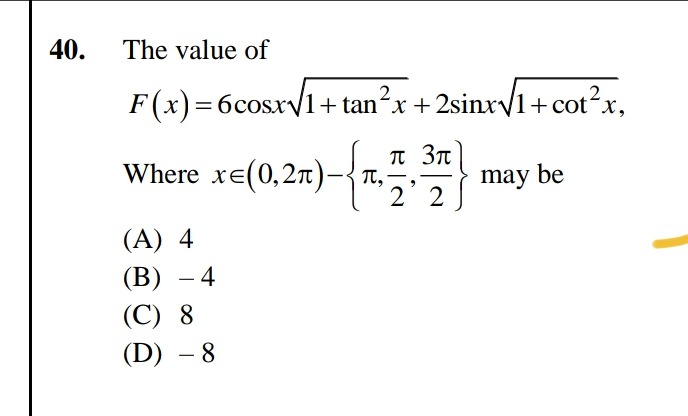
4
-4
8
-8
All options are correct since F(x) can be 4, -4, 8, or -8 depending on the quadrant of x.
Solution
The given function is F(x)=6cosx1+tan2x+2sinx1+cot2x.
We know the trigonometric identities: 1+tan2x=sec2x 1+cot2x=csc2x
Substituting these into the expression for F(x): F(x)=6cosxsec2x+2sinxcsc2x
Using the property A2=∣A∣, we get: F(x)=6cosx∣secx∣+2sinx∣cscx∣
We know that secx=cosx1 and cscx=sinx1. The domain given is x∈(0,2π)−{π,2π,23π}. This means cosx=0 and sinx=0.
We need to consider the signs of cosx and sinx in different quadrants to evaluate the absolute values.
Term 1: 6cosx∣secx∣
- If cosx>0 (i.e., x is in Quadrant I or Quadrant IV), then secx>0, so ∣secx∣=secx. In this case, 6cosx∣secx∣=6cosx(cosx1)=6.
- If cosx<0 (i.e., x is in Quadrant II or Quadrant III), then secx<0, so ∣secx∣=−secx. In this case, 6cosx∣secx∣=6cosx(−cosx1)=−6.
Term 2: 2sinx∣cscx∣
- If sinx>0 (i.e., x is in Quadrant I or Quadrant II), then cscx>0, so ∣cscx∣=cscx. In this case, 2sinx∣cscx∣=2sinx(sinx1)=2.
- If sinx<0 (i.e., x is in Quadrant III or Quadrant IV), then cscx<0, so ∣cscx∣=−cscx. In this case, 2sinx∣cscx∣=2sinx(−sinx1)=−2.
Now, let's combine these possibilities based on the quadrant x lies in:
-
If x∈(0,2π) (Quadrant I): cosx>0 and sinx>0. F(x)=6+2=8.
-
If x∈(2π,π) (Quadrant II): cosx<0 and sinx>0. F(x)=−6+2=−4.
-
If x∈(π,23π) (Quadrant III): cosx<0 and sinx<0. F(x)=−6−2=−8.
-
If x∈(23π,2π) (Quadrant IV): cosx>0 and sinx<0. F(x)=6−2=4.
Thus, the possible values of F(x) are 8,−4,−8,4. All the given options (A) 4, (B) -4, (C) 8, and (D) -8 are possible values for F(x).
