Question
Question: The value of $\cos^{-1}(\frac{-1}{2}) + \cos^{-1}(\frac{1}{2})$ is...
The value of cos−1(2−1)+cos−1(21) is
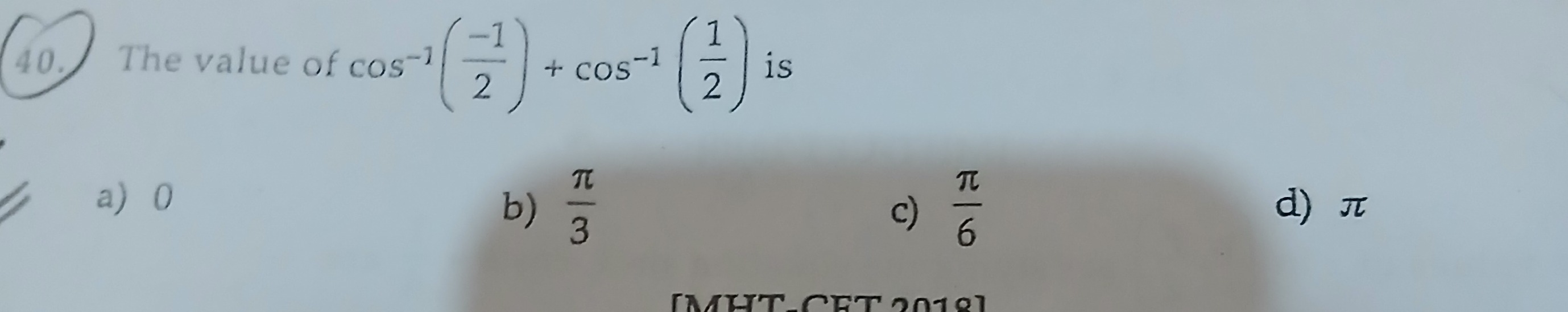
A
0
B
3π
C
6π
D
π
Answer
π
Explanation
Solution
We know that:
cos−1(21)=3πandcos−1(2−1)=32π(in [0,π]).Thus, the sum is:
32π+3π=π.