Solveeit Logo
Login

Question

Question: If $\sin \theta = 3\sin (\theta + 2\alpha)$ and $\tan (\theta + \alpha) = K. \tan \alpha$, then K =...

If sin⁡θ=3sin⁡(θ+2α)\sin \theta = 3\sin (\theta + 2\alpha) and tan⁡(θ+α)=K.tan⁡α\tan (\theta + \alpha) = K. \tan \alpha, then K =

A

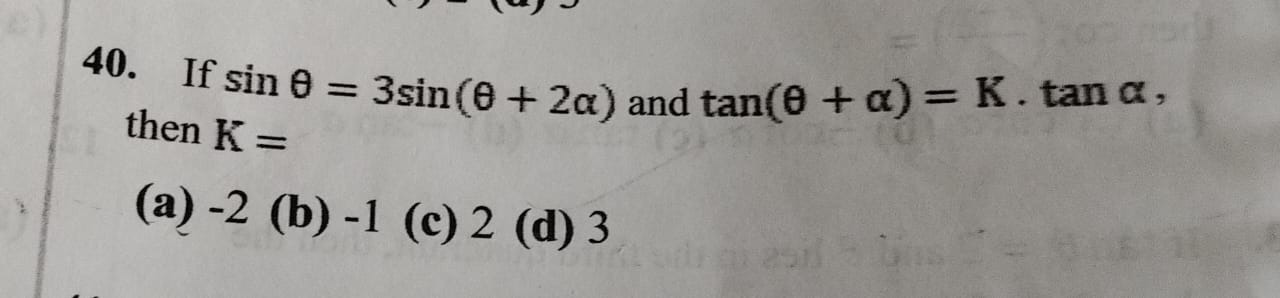
-2

B

-1

C

2

D

3

Answer

-2

Explanation

Solution

The problem asks us to find the value of KK given the relation sin⁡θ=3sin⁡(θ+2α)\sin \theta = 3\sin (\theta + 2\alpha) and tan⁡(θ+α)=K.tan⁡α\tan (\theta + \alpha) = K. \tan \alpha.

Given the equation: sin⁡θ=3sin⁡(θ+2α)\sin \theta = 3\sin (\theta + 2\alpha)

Rearrange the equation to form a ratio: sin⁡θsin⁡(θ+2α)=31\frac{\sin \theta}{\sin (\theta + 2\alpha)} = \frac{3}{1}

Apply the Componendo-Dividendo rule, which states that if ab=cd\frac{a}{b} = \frac{c}{d}, then a+ba−b=c+dc−d\frac{a+b}{a-b} = \frac{c+d}{c-d}. sin⁡θ+sin⁡(θ+2α)sin⁡θ−sin⁡(θ+2α)=3+13−1\frac{\sin \theta + \sin (\theta + 2\alpha)}{\sin \theta - \sin (\theta + 2\alpha)} = \frac{3+1}{3-1} sin⁡θ+sin⁡(θ+2α)sin⁡θ−sin⁡(θ+2α)=42\frac{\sin \theta + \sin (\theta + 2\alpha)}{\sin \theta - \sin (\theta + 2\alpha)} = \frac{4}{2} sin⁡θ+sin⁡(θ+2α)sin⁡θ−sin⁡(θ+2α)=2\frac{\sin \theta + \sin (\theta + 2\alpha)}{\sin \theta - \sin (\theta + 2\alpha)} = 2

Now, use the sum-to-product and difference-to-product trigonometric identities: sin⁡A+sin⁡B=2sin⁡(A+B2)cos⁡(A−B2)\sin A + \sin B = 2\sin\left(\frac{A+B}{2}\right)\cos\left(\frac{A-B}{2}\right) sin⁡A−sin⁡B=2cos⁡(A+B2)sin⁡(A−B2)\sin A - \sin B = 2\cos\left(\frac{A+B}{2}\right)\sin\left(\frac{A-B}{2}\right)

Let A=θA = \theta and B=θ+2αB = \theta + 2\alpha. Then, A+B2=θ+(θ+2α)2=2θ+2α2=θ+α\frac{A+B}{2} = \frac{\theta + (\theta + 2\alpha)}{2} = \frac{2\theta + 2\alpha}{2} = \theta + \alpha. And, A−B2=θ−(θ+2α)2=−2α2=−α\frac{A-B}{2} = \frac{\theta - (\theta + 2\alpha)}{2} = \frac{-2\alpha}{2} = -\alpha.

Substitute these into the equation: 2sin⁡(θ+α)cos⁡(−α)2cos⁡(θ+α)sin⁡(−α)=2\frac{2\sin(\theta + \alpha)\cos(-\alpha)}{2\cos(\theta + \alpha)\sin(-\alpha)} = 2

Since cos⁡(−α)=cos⁡(α)\cos(-\alpha) = \cos(\alpha) and sin⁡(−α)=−sin⁡(α)\sin(-\alpha) = -\sin(\alpha): 2sin⁡(θ+α)cos⁡(α)−2cos⁡(θ+α)sin⁡(α)=2\frac{2\sin(\theta + \alpha)\cos(\alpha)}{-2\cos(\theta + \alpha)\sin(\alpha)} = 2

Simplify the expression: −sin⁡(θ+α)cos⁡(θ+α)⋅cos⁡(α)sin⁡(α)=2-\frac{\sin(\theta + \alpha)}{\cos(\theta + \alpha)} \cdot \frac{\cos(\alpha)}{\sin(\alpha)} = 2 −tan⁡(θ+α)⋅cot⁡(α)=2-\tan(\theta + \alpha) \cdot \cot(\alpha) = 2

Recall that cot⁡(α)=1tan⁡(α)\cot(\alpha) = \frac{1}{\tan(\alpha)}: −tan⁡(θ+α)⋅1tan⁡(α)=2-\tan(\theta + \alpha) \cdot \frac{1}{\tan(\alpha)} = 2 tan⁡(θ+α)=−2tan⁡(α)\tan(\theta + \alpha) = -2\tan(\alpha)

We are given that tan⁡(θ+α)=K.tan⁡α\tan (\theta + \alpha) = K. \tan \alpha. Comparing this with our derived equation, tan⁡(θ+α)=−2tan⁡(α)\tan(\theta + \alpha) = -2\tan(\alpha), we find that K=−2K = -2.