Question

If $\int \frac{dx}{(x^2 + x + 1)^2} = a \tan^{-1} (\frac{2x+1}{\sqrt{3}}) + b (\frac{2x+1}{x^2+x+1}) + C, x > 0$ where C is the constant of integration, then the value of $9(\sqrt{3}a + b)$ is equal to

Answer 1

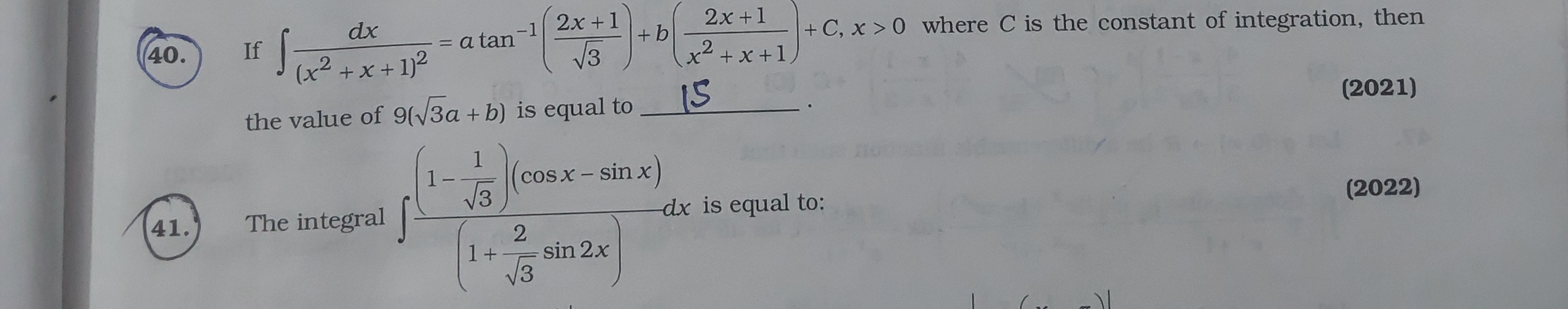
15

Answer 2

The given integral is $\int \frac{dx}{(x^2 + x + 1)^2}$.

We can rewrite the denominator by completing the square: $x^2 + x + 1 = (x + \frac{1}{2})^2 + (\frac{\sqrt{3}}{2})^2$. Let $x + \frac{1}{2} = t$. Then $dx = dt$. The integral becomes $I = \int \frac{dt}{(t^2 + (\frac{\sqrt{3}}{2})^2)^2}$. This is of the form $\int \frac{dt}{(t^2 + p^2)^2}$ where $p = \frac{\sqrt{3}}{2}$.

We use the reduction formula for $I_n = \int \frac{dx}{(x^2+p^2)^n}$: $I_n = \frac{x}{2p^2(n-1)(x^2+p^2)^{n-1}} + \frac{2n-3}{2p^2(n-1)} I_{n-1}$. For our case, $n=2$ and $p^2 = \frac{3}{4}$. $I_2 = \frac{t}{2(\frac{3}{4})(2-1)(t^2+\frac{3}{4})^{2-1}} + \frac{2(2)-3}{2(\frac{3}{4})(2-1)} I_1$ $I_2 = \frac{t}{\frac{3}{2}(t^2+\frac{3}{4})} + \frac{1}{\frac{3}{2}} I_1$ $I_2 = \frac{2t}{3(t^2+\frac{3}{4})} + \frac{2}{3} I_1$.

Now, we need to evaluate $I_1 = \int \frac{dt}{t^2 + \frac{3}{4}}$. This is a standard integral form $\int \frac{dx}{x^2+a^2} = \frac{1}{a} \tan^{-1}(\frac{x}{a})$. Here, $a = \frac{\sqrt{3}}{2}$. $I_1 = \frac{1}{\frac{\sqrt{3}}{2}} \tan^{-1} \left(\frac{t}{\frac{\sqrt{3}}{2}}\right) = \frac{2}{\sqrt{3}} \tan^{-1} \left(\frac{2t}{\sqrt{3}}\right)$.

Substitute $I_1$ back into the expression for $I_2$: $I_2 = \frac{2t}{3(t^2+\frac{3}{4})} + \frac{2}{3} \left( \frac{2}{\sqrt{3}} \tan^{-1} \left(\frac{2t}{\sqrt{3}}\right) \right) + C$ $I_2 = \frac{2t}{3(t^2+\frac{3}{4})} + \frac{4}{3\sqrt{3}} \tan^{-1} \left(\frac{2t}{\sqrt{3}}\right) + C$.

Now, substitute back $t = x + \frac{1}{2} = \frac{2x+1}{2}$. So $2t = 2x+1$. And $t^2+\frac{3}{4} = (x+\frac{1}{2})^2 + \frac{3}{4} = x^2+x+\frac{1}{4}+\frac{3}{4} = x^2+x+1$. Also, $\frac{4}{3\sqrt{3}} = \frac{4\sqrt{3}}{3 \cdot 3} = \frac{4\sqrt{3}}{9}$.

Substituting these back into $I_2$: $I = \frac{2(2x+1)/2}{3(x^2+x+1)} + \frac{4\sqrt{3}}{9} \tan^{-1} \left(\frac{2x+1}{\sqrt{3}}\right) + C$ $I = \frac{2x+1}{3(x^2+x+1)} + \frac{4\sqrt{3}}{9} \tan^{-1} \left(\frac{2x+1}{\sqrt{3}}\right) + C$.

Comparing this with the given form: $\int \frac{dx}{(x^2 + x + 1)^2} = a \tan^{-1} (\frac{2x+1}{\sqrt{3}}) + b (\frac{2x+1}{x^2+x+1}) + C$ We identify the coefficients: $a = \frac{4\sqrt{3}}{9}$ $b = \frac{1}{3}$.

We need to find the value of $9(\sqrt{3}a + b)$. $9(\sqrt{3}a + b) = 9 \left( \sqrt{3} \cdot \frac{4\sqrt{3}}{9} + \frac{1}{3} \right)$ $= 9 \left( \frac{4 \cdot 3}{9} + \frac{1}{3} \right)$ $= 9 \left( \frac{12}{9} + \frac{1}{3} \right)$ $= 9 \left( \frac{4}{3} + \frac{1}{3} \right)$ $= 9 \left( \frac{5}{3} \right)$ $= 3 \cdot 5 = 15$.

The calculated value is 15, which matches the value given in the question.