Question
Question: $\forall$ x $\in$ R find the range of the function, f(x) = cos x (sin x + $\sqrt{sin^2 x + sin^2 \al...
∀ x ∈ R find the range of the function, f(x) = cos x (sin x + sin2x+sin2α); α ∈ [0,π]
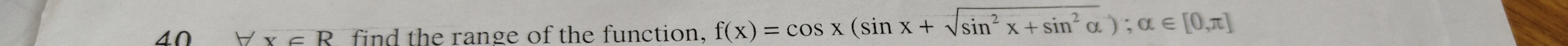
The range of f(x) is [−1+sin2α,1+sin2α]
Solution
Let the given function be f(x)=cosx(sinx+sin2x+sin2α). Let k=sinα. Since α∈[0,π], k∈[0,1].
Case 1: k=0 (i.e., sinα=0) In this case, f(x)=cosx(sinx+sin2x)=cosx(sinx+∣sinx∣).
- If sinx≥0, then f(x)=cosx(2sinx)=sin(2x). The range of sin(2x) is [−1,1].
- If sinx<0, then f(x)=cosx(sinx−sinx)=0. Combining these, the range of f(x) when sinα=0 is [−1,1].
Case 2: k>0 (i.e., sinα∈(0,1]) Let u=sinx and v=cosx. The function is f(x)=v(u+u2+k2). Consider the term g(u)=u+u2+k2. For any real u, u2+k2>u2=∣u∣.
- If u≥0, g(u)=u+u2+k2>u+u=2u≥0.
- If u<0, g(u)=u+u2+k2=−∣u∣+u2+k2. Since u2+k2>∣u∣, g(u)>0. Thus, g(u)>0 for all u∈R. This implies that the sign of f(x) is determined by the sign of cosx. Since cosx can be positive, negative, or zero, f(x) can take positive, negative, or zero values. Due to the symmetry of sinx and cosx over 2π period, the range will be symmetric about 0, i.e., of the form [−M,M] where M=max∣f(x)∣.
To find M, we find the maximum value of f2(x): f2(x)=cos2x(sinx+sin2x+k2)2. Let sinx=ksinht. This substitution is valid for all sinx∈[−1,1] as long as k∈(0,1]. Then sin2x+k2=k2sinh2t+k2=ksinh2t+1=kcosht (since k>0 and cosht>0). So, sinx+sin2x+k2=ksinht+kcosht=k(sinht+cosht)=ket. Now, f(x)=cosx⋅ket. We have cos2x=1−sin2x=1−k2sinh2t. So, f2(x)=(1−k2sinh2t)(ket)2=k2e2t(1−k2sinh2t). Substitute sinht=2et−e−t: f2(x)=k2e2t(1−k2(2et−e−t)2) f2(x)=k2e2t(1−k24e2t+e−2t−2) f2(x)=4k2(4e2t−k2(e4t+1−2e2t)) f2(x)=4k2(−k2e4t+(4+2k2)e2t−k2). Let z=e2t. Since sinx=ksinht∈[−1,1], we have sinht∈[−1/k,1/k]. This implies t∈[arsinh(−1/k),arsinh(1/k)]. Let t0=arsinh(1/k). So t∈[−t0,t0]. Thus z=e2t∈[e−2t0,e2t0]. Consider the quadratic function h(z)=−k2z2+(4+2k2)z−k2. This is a downward-opening parabola. The maximum of h(z) occurs at z=−2(−k2)4+2k2=2k24+2k2=k22+k2=1+k22. The maximum value of h(z) is h(1+k22)=−k2(1+k22)2+(4+2k2)(1+k22)−k2 =−k2(k2k2+2)2+2(2+k2)(k2k2+2)−k2 =−k2(k2+2)2+k22(k2+2)2−k2 =k2(k2+2)2−k2=k2k4+4k2+4−k4=k24k2+4=4(1+k21). Now, we need to check if z=1+k22 is within the domain [e−2t0,e2t0]. e2t0=e2arsinh(1/k)=e2ln(k1+k21+1)=(k1+1+k2)2=k21+1+k2+21+k2=k22+k2+21+k2. Since k>0, 21+k2>0. Thus, k22+k2+21+k2>k22+k2=1+k22. So, the maximum of h(z) occurs within the valid range of z. The maximum value of f2(x) is 4k2⋅4(1+k21)=k2(1+k21)=k2+1. Therefore, the maximum value of ∣f(x)∣ is k2+1=1+sin2α. Since f(x) is continuous and can take positive, negative, and zero values, its range is [−1+sin2α,1+sin2α]. This result also covers Case 1, as for sinα=0, the range becomes [−1+0,1+0]=[−1,1].
Therefore, the range of the function is [−1+sin2α,1+sin2α].
