Question
Question: For shown situation find the maximum elongation in the spring. Neglect friction everywhere. Initiall...
For shown situation find the maximum elongation in the spring. Neglect friction everywhere. Initially, the blocks are at rest and spring is unstretched.
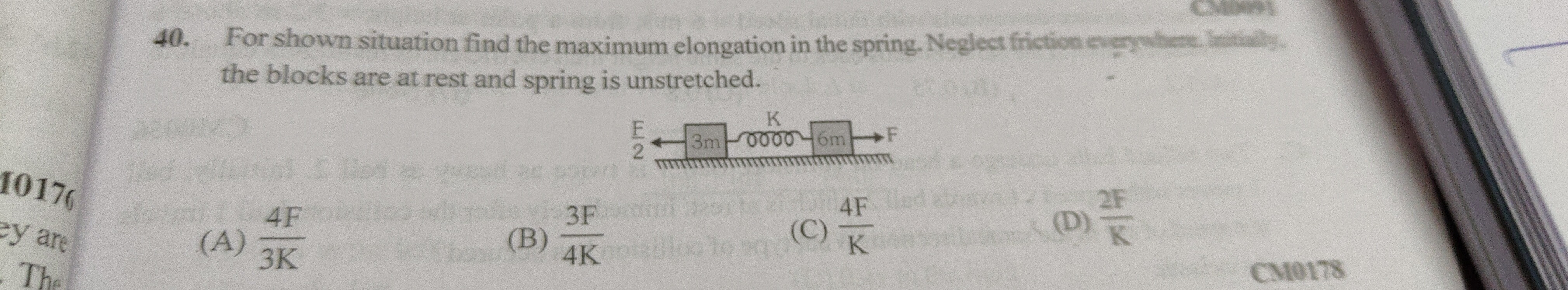
3K4F
4K3F
K4F
K2F
3K4F
Solution
The problem asks for the maximum elongation in the spring for the given system.
The system consists of two blocks with masses m1=3m and m2=6m, connected by a spring with spring constant K. An external force F1=F/2 is applied to the left on block m1, and an external force F2=F is applied to the right on block m2. Initially, the blocks are at rest and the spring is unstretched. Friction is negligible.
We need to analyze the relative motion of the two blocks. Let x be the elongation of the spring, so x=x2−x1, where x1 and x2 are the displacements of block m1 and m2 respectively from their initial positions.
Let's write down the equations of motion for each block:
For block m1 (mass 3m): The forces acting on m1 are the applied force F/2 (to the left) and the spring force Kx (to the right, assuming x is positive for elongation).
3ma1=Kx−F/2 (Equation 1)
For block m2 (mass 6m): The forces acting on m2 are the applied force F (to the right) and the spring force Kx (to the left).
6ma2=F−Kx (Equation 2)
The relative acceleration arel=a2−a1. Substitute a1=3mKx−F/2 and a2=6mF−Kx into the expression for arel:
arel=6mF−Kx−3mKx−F/2
To combine the terms, find a common denominator (which is 6m):
arel=6m(F−Kx)−2(Kx−F/2)
arel=6mF−Kx−2Kx+F
arel=6m2F−3Kx
We know that arel=dt2d2x. So, the equation of motion for the relative displacement x is:
dt2d2x=6m2F−3Kx
This can be rewritten as:
6mdt2d2x=2F−3Kx
This equation describes the motion of the relative coordinate x. It is a form of simple harmonic motion (SHM). To make it more explicit, divide by 3:
2mdt2d2x=32F−Kx
Let μ=2m be the reduced mass for this effective single-body oscillation.
μdt2d2x=32F−Kx
This equation can be written as μdt2d2x=−K(x−xeq), where xeq is the equilibrium position for the oscillation. Comparing this with our equation:
−K(x−xeq)=32F−Kx
−Kx+Kxeq=32F−Kx
Kxeq=32F
xeq=3K2F
The system starts from rest with the spring unstretched. This means at t=0, x=0 and the relative velocity dtdx=0.
For a simple harmonic motion, if the initial velocity is zero, the starting position is an extreme position (amplitude) relative to the equilibrium position.
The initial displacement from the equilibrium position is x(0)−xeq=0−3K2F=−3K2F.
The amplitude of oscillation A is the magnitude of this initial displacement from equilibrium:
A=−3K2F=3K2F.
The maximum elongation in the spring occurs at the other extreme of the oscillation, which is xeq+A.
xmax=xeq+A=3K2F+3K2F
xmax=3K4F
